Liaisons mécaniques avec frottement

modèle parfait et avec frottement

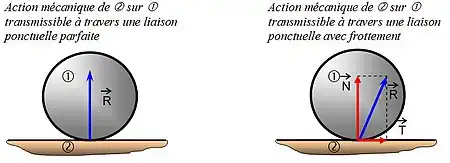
Dans un contact parfait, l’action mécanique transmissible par obstacle entre 2 solides ne peut être en tout point que normale au contact (perpendiculaire au plan tangent commun du contact). Pour que cette action mécanique puisse prendre une autre direction, il y a nécessité d’une composante tangentielle qui ne sera pas transmise par obstacle mais par frottement ou adhérence.

La force résultante transmise dans ce contact se projette suivant une composante normale, dite effort presseur, et une composante tangentielle dite force de frottement.

Il n'est pas toujours nécessaire de distinguer ces composantes lors d'une étude statique (voir lois de Coulomb ci-dessous).

On a deux types de contacts : réparti et engendré.

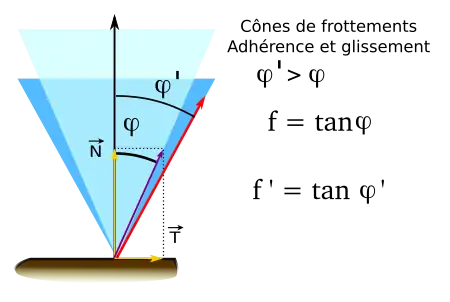
Si on considère deux corps en contact ponctuel avec frottement, il y a 2 situations à observer selon que le glissement entre les deux corps est avéré ou pas.

Si les corps ne glissent pas, la droite d’action transmissible peut s’écarter de la normale de contact jusqu’à une limite fixe (en rouge sur la figure). Le domaine ainsi délimité prend la forme d’un cône dit « cône de frottement d’adhérence ». Le demi angle au sommet est appelé angle d’adhérence. L'étude du cas à la frontière du cône est appelé équilibre strict.

Si la vitesse relative entre les corps devient non nulle, alors la droite d’action prend une inclinaison fixe (violet). On définit de même le « cône de frottement de glissement ».

En général, le cône de glissement est inclus à l’intérieur du cône d’adhérence. Chacun a fait l’expérience de pousser une armoire et de s’apercevoir qu’il est moins dur d’entretenir son glissement, une fois qu’elle a décollé. C’est aussi cette différence qui explique le broutement des chaises qu’on traîne, le sifflement des freins, ou la génération du son des violons et autres instruments à archet. À une bien plus grande échelle, les séismes en sont les conséquences.

Pour certains couples de matériaux, le coefficient d'adhérence est au contraire plus faible que le coefficient de frottement, celui-ci augmentant plus ou moins notablement avec la vitesse de glissement. Ce comportement est recherché pour la conception de nombreux mécanismes industriels afin d'introduire une certaine sécurité intrinsèque et surtout de limiter les vibrations ; voir à ce sujet le wikilivre de tribologie et plus spécialement les chapitres consacrés à la modélisation des actions de contact, aux embrayages, aux freins, etc.

Dans les deux situations précédentes, la direction de l’action transmissible est connue :

• soit parce que le glissement est avéré ;
• soit parce que l'équilibre est avéré ; l'étude statique permet alors la détermination préalable de toutes les actions mécaniques.

Nous pouvons écrire alors une relation entre l’effort presseur (composante normale N) et l’effort de frottement (composante tangentielle T) : elle doit vérifier les lois de Coulomb.

• Cas du glissement avéré :
  • ${\displaystyle T=N\tan {\phi }=Nf}$ où ${\displaystyle f=\tan {\phi }}$ est appelé coefficient de frottement de glissement.
  • le sens de T est tel qu'il s'oppose au glissement.
• Cas d'équilibre avéré :
  • ${\displaystyle T\leq N\tan {\phi '}=Nf'}$ où ${\displaystyle f'=\tan {\phi '}}$ est appelé coefficient de frottement d’adhérence.
  • si l'inégalité n'est pas vérifiée, c'est que l'hypothèse d'équilibre doit être remise en question (glissement).
  • Le sens de T est normalement induit par l'étude. Dans le cas de l'équilibre strict, il est arbitrairement choisi pour s'opposer au glissement probable des deux pièces.

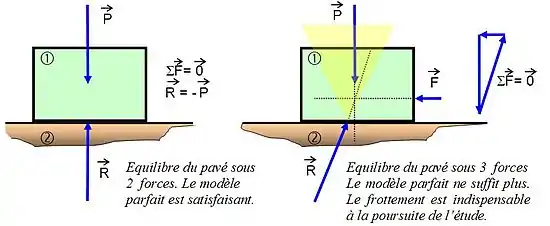
En considérant un pavé posé sur une surface plane. Si le sol est bien à niveau alors l’équilibre du pavé est possible et les forces poids ${\displaystyle {\vec {P}}}$ et réaction du sol ${\displaystyle {\vec {R}}}$ s’annulent (voir statique).

Pour déplacer ce pavé, on exerce une force latérale ${\displaystyle {\vec {F}}}$. Tant que le pavé reste en place, son équilibre est toujours vrai ; ce qui impose la relation d’équilibre entre les trois forces (Principe fondamental de la statique). On remarque alors que l’action du sol n’est plus normale au contact. Il y a donc nécessairement du frottement.

Le problème reste alors entier : Peut-on connaître l’intensité de la force permettant de faire bouger le pavé, quand la seule donnée est le poids du pavé ?

On remarquera aussi que le point d'application de ${\displaystyle {\vec {F}}}$ modifie la position de la réaction au sol. Plus ${\displaystyle {\vec {F}}}$ est appliqué haut, plus l'appui au sol se fait vers l'avant. Dans le cas d'un objet très haut, une armoire par exemple, il se peut que la réaction du sol soit portée à l'extérieur (ce qui n'est pas possible, puisque cela impliquerait des actions locales de signe opposé). L'équilibre n'étant plus possible, alors il y a basculement.

La valeur de ces coefficients n’est pas modélisable et ne peut s’établir que par la mesure. On trouvera de nombreuses valeurs directement applicables dans le wikilivre de tribologie.

Selon les lois de Coulomb, qui constituent un premier modèle simpliste mais souvent suffisant, ces valeurs ne dépendent que de la nature des matériaux mis en présence et de l'état de leurs surfaces ; elles sont indépendantes des formes des surfaces de contact, de leurs dimensions, des pressions de contact et de la vitesse de glissement. La complexité du modèle doit être adaptée au besoin. La tribologie indique l'ensemble des facteurs à considérer si un modèle trop simple ne convenait pas.

La différence entre le coefficient de frottement et le coefficient d'adhérence étant souvent faible, les deux valeurs peuvent être confondues. Voici quelques valeurs numériques pour les coefficients d’adhérence (glissement) :

• Acier / acier : 0,2 (0,15)- 0.3
• Acier / glace : 0,02 (0,02)
• Acier / bronze : 0,1 (0,05)
• Acier / garnitures de freins : 0,4 (0,25) (pression maxi 20 MPa, T° < 200 °C)
• Pneu / route sèche : 0,8 (0,5)
• Pneu / route mouillée : 0,5 (0,35)

Dans un problème de statique, la considération du frottement ne doit pas être prise en compte si le phénomène est considéré comme négligeable. Avec un coefficient inférieur à 0,1 les droites d’action sont peu déviées (par rapport au modèle parfait), de ce fait le résultat final est peu perturbé.

Cependant le frottement doit être considéré quand on souhaite déterminer son influence sur le problème étudié, où lorsque le modèle parfait n’apporte pas de solution possible (pavé qu’on pousse mais qui cependant reste immobile). Dans ce cas 2 types d’étude sont à envisager :

1- Hypothèse de liaison avec frottement d’adhérence : l’étude est menée dans un premier temps pour déterminer l’ensemble des forces. L’hypothèse de liaison avec frottement accorde des libertés supplémentaires aux directions des droites d’action. Puis dans un deuxième temps, on vérifie que les liaisons avec frottement sont dans une situation compatible avec les lois de Coulomb (droites d’action à l’intérieur des cônes d’adhérence). Si ce n’est pas le cas, l’équilibre n’est pas possible. Il faut alors revoir la géométrie du problème.

2- Hypothèse d’équilibre strict : Quand les données sont insuffisantes, il est intéressant de poser l’hypothèse de glissement (contradictoire avec la notion d'équilibre). On fixe ainsi arbitrairement la direction de certaines actions mécaniques. Le résultat correspond alors à la situation limite au-delà de laquelle l’équilibre n’est plus possible. Cette hypothèse est aussi naturelle quand il s’agit de calculer les performances d’un système de freinage ou d’embrayage, dans ce cas les accélérations sont souvent supposées nulles ce qui élimine les considérations inertielles.

Le tracé du cône de frottement est inévitable dans les deux cas; Or la caractéristique donnée est le coefficient de frottement (tangente de l’angle). Cela est possible sans calcul en utilisant la méthode suivante (qui s’appuie sur les relations dans le triangle rectangle : tan = côté opposé / côté adjacent) :

Méthode de tracé du cône de frottement

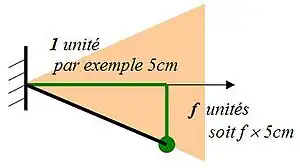
1. monter de 1 unité sur la normale de contact,
2. tourner de la valeur du coefficient,
3. tracer le bord du cône.

Cette méthode est plus précise que celle qui consiste à calculer l’angle puis le reporter, car les valeurs usuelles de coefficient sont voisines et les rapporteurs d’angle souvent limités en précision au demi degré.

• Le wikilivre de tribologie et plus spécialement le chapitre consacré à la modélisation des actions de contact.
• Arc-boutement
• Résistance au roulement