Lemme d'Ogden

Étant donné un mot ${\displaystyle w=a_{1}a_{2}\cdots a_{n}}$, où les ${\displaystyle a_{i}}$ sont des lettres, on appelle position dans ${\displaystyle w}$ tout entier de l'ensemble ${\displaystyle \{1,2,\ldots ,n\}}$. Un choix de ${\displaystyle N}$ positions distinguées ou positions marquées dans ${\displaystyle w}$ (ceci est la terminologie traditionnelle) est simplement un sous-ensemble ${\displaystyle I\subset \{1,2,\ldots ,n\}}$ de positions contenant ${\displaystyle N}$ éléments. Avec ces définitions, le lemme s'énonce comme suit :

Le plus petit entier ${\displaystyle N}$ pour lequel l'énoncé est vrai est appelé la constante d'Ogden.

Il existe une variante grammaticale du lemme d'Ogden : elle dit que la paire itérante ${\displaystyle (x,u,y,v,z)}$ peut être choisie grammaticale. Cette variante est bien utile dans certains cas, et notamment pour les langages inhéremment ambigus. Voici l'énoncé :

Dans cet énoncé, le mot ${\displaystyle w}$ peut contenir des variables de la grammaire : il appartient au « langage élargi » constitué par définition de tous les mots dérivant de ${\displaystyle S}$, qu'ils contiennent ou non des variables.

• Le langage ${\displaystyle L=\{a^{n}b^{n}c^{n}\mid n\geqslant 0\}}$ n'est pas algébrique. Pour le voir, on distingue dans le mot ${\displaystyle a^{N}b^{N}c^{N}}$ les lettres égales à ${\displaystyle a}$. En appliquant le lemme, on fait varier le nombre de lettres ${\displaystyle a}$. Il faut distinguer encore le cas où le facteur ${\displaystyle v}$ est vide ou non, mais comme on itère ce facteur, il ne peut être formé que de lettres de même type, et on ne peut pas compenser l'accroissement de lettres ${\displaystyle b}$ et ${\displaystyle c}$ à la fois, d'où la contradiction.

• Le langage ${\displaystyle L=\{a^{m}b^{n}c^{m}d^{n}\mid n,m\geq 0\}}$ n’est pas algébrique. On applique cette fois la variante grammaticale du lemme au mot ${\displaystyle w=a^{N}b^{N}c^{N}d^{N}}$, où ${\displaystyle N}$ est la constante d'Ogden, et où les lettres distinguées sont les lettres ${\displaystyle b}$. Il existe des dérivations

${\displaystyle S{\stackrel {*}{\to }}a^{N}b^{k}Xd^{\ell },\ X{\stackrel {*}{\to }}b^{i}Xd^{i},\ X{\stackrel {*}{\to }}b^{\bar {k}}c^{N}d^{\bar {\ell }}}$

avec ${\displaystyle N=k+i+{\bar {k}}=\ell +i+{\bar {\ell }}}$. On applique le lemme une deuxième fois, au mot ${\displaystyle a^{N}b^{k}Xd^{\ell }}$, où cette fois-ci ce sont les lettres ${\displaystyle a}$ qui sont distinguées. On obtient une paire itérante contenant des lettres ${\displaystyle a}$ itérées, mais aucune lettre ${\displaystyle d}$, contradiction.

Le lemme d'Odgen est une condition nécessaire mais pas suffisante pour les langages algébriques.

• Le langage ${\displaystyle L=\{a^{n}b^{m}\mid n\neq m\}\cup \{a^{n}b^{n}\mid n{\text{ non premier }}\}}$ n’est pas algébrique, car étant un langage borné sur un alphabet à deux lettres, son complément (par rapport à ${\displaystyle a^{*}b^{*}}$) est ${\displaystyle \{a^{n}b^{n}\mid n{\text{ premier }}\}}$ qui n’est pas algébrique. Pourtant, le langage vérifie le lemme d'Ogden[2].
• Le langage ${\displaystyle L=b^{*}\cup aaa^{*}b^{*}\cup \{ab^{p}\mid p{\text{ premier }}\}}$ n'est pas algébrique, mais le lemme d'Ogden ne permet pas de le prouver parce qu'il n'y a pas moyen d'éviter d'itérer la lettre ${\displaystyle a}$ initiale [3].

• Le langage ${\displaystyle L=\{a^{n}b^{n}c^{m}\mid n,m\geq 0\}\cup \{a^{m}b^{n}c^{n}\mid n,m\geq 0\}}$ est inhéremment ambigu. Un langage est inhéremment ambigu si toutes les grammaires qui l'engendrent sont ambiguës. On applique une première fois la variante du lemme au mot ${\displaystyle w=a^{N}b^{N}c^{N+N!}}$ où ${\displaystyle N}$ est la constante d'Ogden, et en distinguant les lettres ${\displaystyle b}$. Il existe une dérivation ${\displaystyle S{\stackrel {*}{\to }}xXz{\stackrel {*}{\to }}xuXvz{\stackrel {*}{\to }}xuyvz}$, et les conditions impliquent que ${\displaystyle u=a^{i}}$ et ${\displaystyle v=b^{i}}$ pour un entier ${\displaystyle 0\leq i\leq N}$. En itérant ${\displaystyle N!/i}$ fois la dérivation ${\displaystyle X{\stackrel {*}{\to }}uXv}$ on obtient un arbre de dérivation pour le mot ${\displaystyle a^{N+N!}b^{N+N!}c^{N+N!}}$. Cet arbre contient un sous-arbre dont la frontière ne contient que des lettres ${\displaystyle a}$ et ${\displaystyle b}$, dont au moins ${\displaystyle N!-N}$ lettres ${\displaystyle b}$. En appliquant le même procédé au mot ${\displaystyle w=a^{N+N!}b^{N}c^{N}}$, on obtient un autre arbre de dérivation pour le même mot ${\displaystyle a^{N+N!}b^{N+N!}c^{N+N!}}$. Cet arbre contient un sous-arbre dont la frontière ne contient que des lettres ${\displaystyle b}$ et ${\displaystyle c}$, dont au moins ${\displaystyle N!-N}$ lettres ${\displaystyle b}$. Cet arbre est donc différent du premier arbre.

Considérons un arbre dont certaines feuilles sont distinguées. On dit que :

• un nœud est distingué lorsque le sous-arbre dont il est racine contient des feuilles distinguée ;
• un nœud est spécial lorsqu'au moins deux de ses enfants sont distingués.

Le parent d'un nœud distingué est distingué, la racine est distinguée dès que l'une des feuilles est distinguée, un nœud spécial est lui-même distingué.

Un arbre est de degré ${\displaystyle m}$ si chaque nœud a au plus ${\displaystyle m}$ enfants.

Découpage du mot ${\displaystyle w}$. On reste dans le langage en itérant la partie en couleur car ${\displaystyle b_{1}}$ et ${\displaystyle b_{2}}$ sont des nœuds étiquetés par la même variable ${\displaystyle X}$.

On utilise la contraposée du lemme précédent : si l'arbre a strictement plus de ${\displaystyle m^{r}}$ feuilles distinguées, alors l'arbre a au moins une branche qui contient au moins ${\displaystyle 1+r}$ nœuds spéciaux.

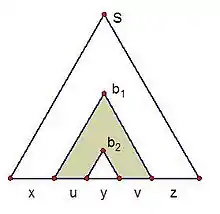
Soit ${\displaystyle m}$ la longueur maximale des membres droits des règles. On pose ${\displaystyle r=2(|V|+1)}$ et ${\displaystyle N=1+m^{r}}$. Considérons un arbre de dérivation pour le mot ${\displaystyle w}$. Par définition, l'arbre est de degré ${\displaystyle m}$ et possède des feuilles distinguées qui sont les positions distinguées de ${\displaystyle w}$. L'arbre possède une branche ayant au moins ${\displaystyle 1+r}$ nœuds spéciaux, notés ${\displaystyle s_{0},\ldots ,s_{r}}$. Chacun de ces nœuds a au moins un fils distingué qui n'est pas sur la branche ; le nœud est gauche si ce fils est à gauche de la branche, il est droit sinon. Comme ${\displaystyle 1+r=2|V|+3}$, il y a au moins ${\displaystyle |V|+2}$ sommets distingués soit tous gauches, soit tous droits. Comme ce nombre est supérieur au nombre de variables, deux sommets ${\displaystyle s_{i}}$ et ${\displaystyle s_{j}}$ (notés ${\displaystyle b_{1}}$ et ${\displaystyle b_{2}}$ sur la figure), avec ${\displaystyle i<j}$, sont étiquetés avec la même variable ${\displaystyle X}$. L'arbre donne alors les dérivations

${\displaystyle S{\stackrel {*}{\to }}xXz}$, ${\displaystyle X{\stackrel {*}{\to }}uXv}$ et ${\displaystyle X{\stackrel {*}{\to }}y}$.

Si les nœuds distingués sont gauche, les mots ${\displaystyle x,u,y}$ contiennent des positions distinguées, sinon c'est le cas des mots ${\displaystyle y,v,z}$. Enfin, si le mot ${\displaystyle y}$ contient plus que ${\displaystyle N}$ positions distinguées, on recommence le découpage à partir de la racine ${\displaystyle s_{j}}$ de son sous-arbre.

• William F. Ogden, « A Helpful Result for Proving Inherent Ambiguity », Mathematical Systems Theory, vol. 2, n^o 3,‎ 1968, p. 191-194 (DOI 10.1007/BF01694004)

• Olivier Carton, Langages formels, calculabilité et complexité, 2008 [détail de l’édition] (lire en ligne)

• (en) Marcus Kracht, « Too Many Languages Satisfy Ogden’s Lemma », University of Pennsylvania Working Papers in Linguistics, vol. 10,‎ 2004

• Grammaire algébrique
• Langage algébrique
• Lemme d'itération pour les langages algébriques