Kakuro

Le kakuro (en japonais : カックロ, kakkuro, abréviation de 加算クロス kasan-cross, « addition en croix ») est un jeu logique que l'on perçoit souvent comme une adaptation numérique des mots croisés. Au Japon, ce jeu est connu sous le nom de Kakkuro et sa popularité est immense. En Grande-Bretagne, The Guardian a commencé à publier ce jeu en septembre 2005. Depuis, beaucoup d'autres journaux britanniques ont suivi et publient quotidiennement une grille.

Un kakuro facile

Solution du kakuro ci-dessus

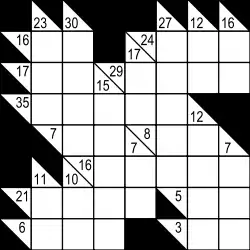
Il est presque identique aux nombres fléchés publiés par Sport cérébral, dans lesquels une même combinaison de chiffres ne peut pas être utilisée deux fois dans la même grille. Aussi, bien que le « Kakuro » soit apparu en France vers 2004-2005 dans le sillage du sudoku, le jeu en lui-même est connu depuis bien plus longtemps.

Description

D'habitude, le jeu utilise une grille comportant des cases remplies (noires) ou vides (blanches), d'une taille 16×16 le plus souvent. Outre la ligne du haut et la colonne de gauche, entièrement noires, la grille, telle une grille de mots-croisés, est divisée en « mots » horizontaux ou verticaux par les cases noires.

Les cases noires elles-mêmes sont divisées en deux par une diagonale allant du coin en haut à gauche au coin en bas à droite, de sorte que le « mot » à sa droite et le « mot » au-dessous puissent être définis dans la même case.

L'objectif du jeu est de remplir les cases vides (blanches) avec des chiffres entre 1 et 9 de sorte que la somme de tous les chiffres d'un nombre soit égale au nombre inscrit dans la case remplie (noire) définissant le nombre, et qu'un nombre ne puisse pas contenir deux fois le même chiffre. Cette dernière règle est celle qui rend possible la création de grilles à solution unique.

Dans la version nombres fléchés publiée par Sport cérébral, une même séquence de chiffres ne peut apparaître qu'une fois par grille. Cette règle rend le jeu logique et permet d'éviter des grilles à plusieurs solutions, alors que seule une de ces solutions est acceptée.

Méthodes de résolution simples

Pour résoudre une grille, il faut commencer en général par trouver une case dont les combinaisons possibles horizontale (somme de la ligne) et verticale (somme de la colonne) ont un seul chiffre commun.

Exemple

Si une ligne de 2 cases dont la somme est 4 croise une colonne de 2 cases dont la somme est 3, alors comme les chiffres sont différents et non nuls :

les seules combinaisons pour la ligne sont 1+3 ou 3+1 ;
les seules combinaisons pour la colonne sont 1+2 ou 2+1;
la case à leur intersection ne peut donc valoir que 1, seul chiffre commun ;
on déduit donc la valeur des autres cases de la ligne et la colonne de cette case ;
et ainsi de suite...

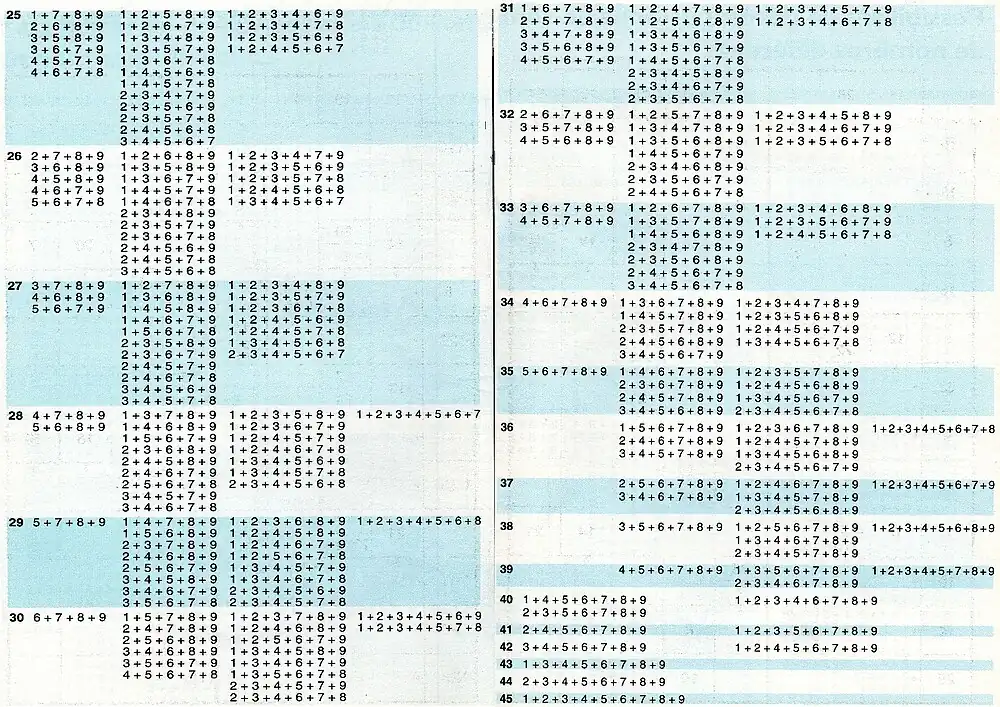
Exemples de sommes possibles

3 avec deux chiffres : 1, 2
4 avec deux chiffres : 1, 3
5 avec deux chiffres : 1, 4 ou 2, 3
6 avec deux chiffres : 1, 5 ou 2, 4
7 avec deux chiffres : 1, 6 ou 2, 5 ou 3, 4
8 avec deux chiffres : 1, 7 ou 2, 6 ou 3, 5
9 avec deux chiffres : 1, 8 ou 2, 7 ou 3, 6 ou 4, 5
10 avec deux chiffres : 1, 9 ou 2, 8 ou 3, 7 ou 4, 6
11 avec deux chiffres : 2, 9 ou 3, 8 ou 4, 7 ou 5, 6
12 avec deux chiffres : 3, 9 ou 4, 8 ou 5, 7
13 avec deux chiffres : 4, 9 ou 5, 8 ou 6, 7
14 avec deux chiffres : 5, 9 ou 6, 8
15 avec deux chiffres : 6, 9 ou 7, 8
16 avec deux chiffres : 7, 9
17 avec deux chiffres : 8, 9
Les nombres supérieurs ou égaux à 18 ne sont pas décomposables avec deux chiffres.
Les nombres inférieurs ou égaux à 5 ne sont pas décomposables avec trois chiffres.
6 avec trois chiffres : 1, 2, 3
7 avec trois chiffres : 1, 2, 4
8 avec trois chiffres : 1, 2, 5 ou 1, 3, 4
...
23 avec trois chiffres : 6, 8, 9
24 avec trois chiffres : 7, 8, 9
Les nombres supérieurs ou égaux à 25 ne sont pas décomposables avec trois chiffres.
Les nombres inférieurs ou égaux à 9 ne sont pas décomposables avec quatre chiffres.
10 avec quatre chiffres : 1, 2, 3, 4
11 avec quatre chiffres : 1, 2, 3, 5
29 avec quatre chiffres : 5, 7, 8, 9
30 avec quatre chiffres : 6, 7, 8, 9
45 : 1, 2, 3, 4, 5, 6, 7, 8, 9 (seul nombre décomposable avec 9 chiffres)

On ne peut pas décomposer un nombre supérieur à 45.

On peut aisément allonger cette liste.

Méthodes de résolution avancées

Comme dans le cas du Sudoku, les puzzles de Kakuro plus durs exigent de recourir à divers types de chaînes.

Un livre récent en anglais Pattern-Based Constraint Satisfaction and Logic Puzzles[1] montre que les techniques développées pour le Sudoku dans un livre plus ancien du même auteur The Hidden Logic of Sudoku[2] se généralisent à n'importe quel problème fini de Satisfaction de Contraintes. Cela inclut les chaînes xy, les fouets (whips) et les tresses (braids).

Ce livre montre aussi en détail comment appliquer ces chaînes au Kakuro. En particulier, il montre que, une fois que des variables additionnelles sont introduites pour représenter les combinaisons des différents secteurs horizontaux ou verticaux compatibles avec leurs contraintes de somme, il existe dans la plupart des cas une solution de logique pure basée sur ces chaînes et ne demandant pas d'autres calculs arithmétiques.

Ces techniques sont implémentés directement sous forme de règles dans la partie KakuRules du logiciel général de satisfaction de contraintes CSP-Rules, désormais disponible sur la plate-forme GitHub : https://github.com/denis-berthier/CSP-Rules-V2.1

Notes et références

(en) Denis Berthier, « Pattern-Based Constraint Satisfaction and Logic Puzzles », Lulu Publishers, (ISBN 978-1-291-20339-4),‎ 20 novembre 2012 (lire en ligne, consulté le 24 octobre 2012)
(en) Denis Berthier, « The Hidden Logic of Sudoku », Lulu Publishers, (ISBN 978-1-84753-472-9),‎ 16 mai 2007 (lire en ligne, consulté le 16 mai 2007)

Bibliographie

(en) Denis Berthier, Pattern-Based Constraint Satisfaction and Logic Puzzles, Paris, Lulu, 2012, 480 p. (ISBN 978-1-291-20339-4, lire en ligne)

Liens externes

(en) Guide pour débutants (Macromedia Flash nécessaire)
De nombreux puzzles logiques, y compris le Kakuro, de degrés de difficulté variés, fournis par atksolutions (Macromedia Flash required)
(en) Description de différentes combinaisons de nombres
(fr) « Assistant permettant de lister les différentes combinaisons de nombres »^{(Archive.org • Wikiwix • Archive.is • Google • Que faire ?)} (consulté le 30 mars 2013)
(fr) Introduction au jeu de Kakuro et exemple complet de résolution
(fr) Tables de partitions des nombres utiles pour résoudre les problèmes de Kakuro
(en) Comment jouer

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.