Interféromètre de Fizeau

L'interféromètre de Fizeau est un montage optique d'interférométrie à division d'amplitude, proposé en 1862 par le physicien français Hippolyte Fizeau[1], dans lequel deux surfaces partiellement réflectrices sont placées face à face et éclairées par un faisceau de lumière cohérente[2]. La lumière réfléchie par la face arrière du premier réflecteur, transparent, est combinée à la lumière réfléchie par la face avant du second. Les deux ondes réfléchies interfèrent entre elles pour créer des franges d'interférence, par exemple sur un écran de projection conjugué optiquement aux réflecteurs. Ces franges, dites "d'égale épaisseur", sont analogues à des lignes de niveau sur une carte topographique et permettent de cartographier avec une grande précision les variations de la distance entre les deux surfaces réflectrices.

Schéma d'un interféromètre de Fizeau

Il ne faut pas confondre l'interféromètre de Fizeau avec les différentes expériences de Fizeau destinées à la mesure de la vitesse de la lumière, ou à la méthode de Fizeau (moyen de séparer deux sources lumineuses ponctuelles proches par interférométrie). L'interféromètre développé spécifiquement par Fizeau pour étudier la vitesse de la lumière dans les milieux en mouvement est présenté en fin d'article.

Application au contrôle de pièces optiques

Les interféromètres de Fizeau sont communément utilisés pour la mesure des surfaces optiques de précision, par exemple au cours de leur fabrication.

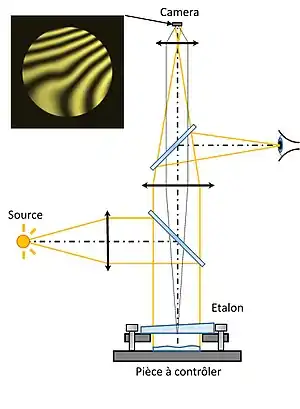
Le plus souvent, la surface d'une lentille ou un miroir en cours de fabrication est comparée à une pièce de référence possédant la forme désirée (plan ou sphère dit « étalon », de grande qualité). La pièce de référence transparente est placée par-dessus l'optique testée, séparée de celle-ci par un support de faible épaisseur et d'orientation réglable. Les faisceaux réfléchis par le plan étalon et la surface à contrôler sont superposés de manière à interférer. L'étalon présente un léger biseau (un angle d'une fraction de degré est suffisant) de manière que la lumière réfléchie par sa face supérieure imparfaite ne produise pas d'interférences supplémentaires dans la figure obtenue. Les franges d'interférence caractérisent alors une épaisseur donnée d'air entre la surface à contrôler et la surface étalon (cf. section Calcul des interférences), donc le défaut de la surface.

Lors de la fabrication d'une lame à faces parallèles, on peut aussi observer les interférences entre les réflexions de chacune des deux faces, afin de vérifier le bon parallélisme de celles-ci. Les franges permettent de remonter dans ce cas aux variations de l'épaisseur totale de la lame.

Dans les deux cas, les échantillons sont illuminés par un faisceau provenant d'une source monochromatique, telle qu'une lampe spectrale ou un laser. En 1862, Fizeau développe pour l'occasion la première lampe à vapeur de sodium. Une lame semi-réfléchissante et des optiques de projection permettent la récupération de la lumière réfléchie et la visualisation des franges.

Calcul des interférences

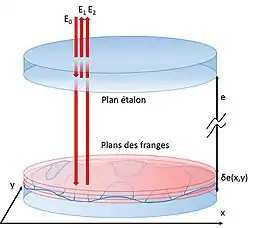
Schéma des franges obtenues à l'intersection entre la surface contrôlée et les plans de différence de marche constante.

Avec E₀ l'éclairement supposé uniforme de l'onde incidente, E₁ = R₁ E₀ celui de l'onde réfléchie par l'étalon, et E₂ = (1-R₁) R₂ E₀ celui l'onde réfléchie par la surface à contrôler, l'éclairement E sur l'écran où l'on projette la figure d'interférence est de la forme :

$E(x,y)=E_{1}+E_{2}+2{\sqrt {E_{1}E_{2}}}\cos {\bigl (}2\pi {\frac {\Delta (x,y)}{\lambda }}{\bigr )}$

avec λ la longueur d'onde et Δ(x,y) la différence de marche entre les deux ondes au point (x,y) d'incidence sur la surface, qui s'écrit :

$\Delta (x,y)=2e+2\delta e(x,y)$

On remarque que le contraste (ou taux de modulation) des franges d'interférences est maximal lorsque E₁ = E₂, donc lorsque les réflectivités R₁ et R₂ des deux surfaces sont équivalentes.

On peut déduire de ces deux équations que les franges sont analogues à des lignes de niveau (d'égale épaisseur entre la surface et l'étalon, quelle que soit la forme de ce dernier), et que l'incrément d'"altitude" séparant chaque frange de la suivante vaut λ/2 (ou λ/2n si le milieu ambiant n'est pas l'air, avec n l'indice de celui-ci). Si la longueur d'onde est du domaine visible (~500 nm), on comprend que l'on pourra visualiser le défaut de surface avec une précision de l'ordre du dixième de micron.

A noter que pour une figure d'interférence statique, on ne peut deviner le sens de l'incrément entre chaque frange, et donc reconstituer le défaut de la surface. Toutefois, en décalant légèrement l'étalon (en diminuant l'épaisseur d'air e par exemple par appui sur le support), on peut faire défiler les franges, celles-ci demeurant à différence de marche constante par rapport à l'étalon (elles vont, si l'on diminue e, se déplacer vers les δe croissants sur la figure).

Interféromètres modernes et mesure par décalage de phase

Interféromètre de Fizeau numérique (marque ZYGO).

Test du miroir de 17 pouces (403 mm de diamètre) de l'observatoire de Cambridge sur un grand interféromètre de Fizeau (chez Grubb Parsons au début du XX^e siècle).

De nos jours, les interféromètres de Fizeau sont commercialisés sous la forme d'instruments intégrés et informatisés[3].

Ils emploient une source laser de grande longueur de cohérence (typiquement un laser He-Ne) qui dispense de limiter l'épaisseur entre l'étalon et la surface mesurée à quelques millimètres comme devait le faire Fizeau.

La méthode de mesure numérique, par décalage de phase[4] - [5], est basée sur le déplacement sub-longueur d'onde de l'étalon et le traitement des figures d'interférence obtenues après chaque déplacement. Elle permet la mesure des défauts de surface au nanomètre près.

Ces instruments ont permis l'avènement de l'optique de précision moderne, capable désormais de produire des miroirs ou lentilles de grande qualité à la chaîne, ou pour les télescopes des optiques de plusieurs mètres (voir ci-contre l'image obtenue sur le télescope de Cambridge au début du vingtième siècle) avec des défauts de surface de l'ordre du nanomètre.

Expérience interférométrique de Fizeau sur la vitesse de la lumière dans les milieux en mouvement

Contexte

En 1851, Fizeau étudie la vitesse de la lumière dans l'eau en mouvement[6], afin de tester l'hypothèse de l'éther luminifère comme medium de propagation de la lumière (hypothèse qui fut mise en échec par les expériences de Michelson et Morley à la fin du XIX^e siècle).

D'après la théorie dominante à l'époque, l'éther était entraîné par le milieu de propagation et se déplaçait avec lui. En conséquence, dans un fluide en mouvement, la lumière devait avoir une vitesse qui était la somme de sa vitesse de propagation dans le fluide et de la vitesse du fluide. En 1818, Augustin Fresnel avait proposé un modèle d'entraînement partiel de l'éther par les milieux denses qui expliquait l'aberration de la lumière (décalage de la position des étoiles vues de la Terre en mouvement) relevée par les astronomes.

Expérience de Fizeau

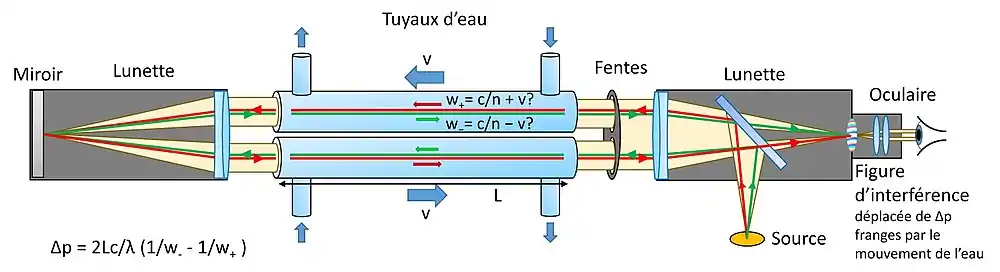
Schéma de l'expérience interférométrique de Fizeau pour l'étude de l'entraînement de l'hypothétique "éther" par le mouvement de l'eau dans deux canalisations.

Dans cette expérience, deux faisceaux lumineux contra-propageants sélectionnés par des fentes sont amenés à parcourir le même chemin dans deux canalisations d'eau, l'un dans le même sens que le courant d'eau, l'autre dans le sens inverse (faisceaux rouge et vert sur le schéma ci-dessus). Ils se recombinent pour former des franges d'interférences (interférences des fentes de Young), visualisées à l'aide un oculaire gradué.

La vitesse de propagation des deux faisceaux dans l'eau est respectivement, dans l'hypothèse d'un éther solidaire du milieu, la composée de la vitesse de la lumière dans l'eau et de la vitesse de l'eau :

$w_{+}=c/n+v$ pour le faisceau rouge,

$w_{-}=c/n-v$ pour le faisceau vert,

où n = 1,33 est l'indice de réfraction de l'eau.

Lorsque l'eau est en mouvement, on observe donc un déplacement des franges d'interférence par rapport au cas où l'eau n'est animée d'aucune vitesse, valant, en fraction de frange :

$\Delta p={\frac {2Lc}{\lambda }}{\biggl (}{\frac {1}{w_{-}}}-{\frac {1}{w_{+}}}{\biggr )}$

où L est la longueur des tuyaux, c est la vitesse de la lumière, λ sa longueur d'onde.

Fizeau s'attend avec son expérience, où L = 1,47 m, et v = 7,07 m/s, à un déplacement de 0,46 franges. Mais il repère un déplacement de seulement 0,23±0,05 franges[6].

Il constate en fait que ce déplacement est celui prédit par l'entraînement partiel de l'éther par le milieu proposé par Fresnel :

$w_{+}=c/n+v(1-1/n^{2})$ ,

qui prévoit un déplacement de 0,20 franges pour l'eau. Plus un milieu est dense (d'indice élevé), plus "l'éther est entraîné", alors que dans l'air le phénomène est insensible.

Albert Michelson et Edward Morley reproduisent l'expérience de Fizeau en 1886 avec un instrument plus stable et plus précis[7], aboutissant au même résultat. En 1915, Pieter Zeeman utilise les canalisations d'eau de la ville d'Amsterdam pour aller encore plus loin en précision, et confirme un effet chromatique prédit par Hendrik Lorentz[8].

Explication

L'expérience ne sera correctement expliquée qu'avec l'avènement de la théorie de la relativité restreinte proposée par Albert Einstein en 1905, qui donne la juste loi de composition des vitesses relativistes.

En effet, la composée w des vitesses u et v dans le cas où tous les vecteurs vitesses sont colinéaires ne s'écrit :

$w=u+v$

que si u et v sont très inférieures à la vitesse de la lumière dans le vide c. Dans le cas contraire :

$w={\frac {u+v}{1+uv/c^{2}}}$ .

En 1907, Max von Laue montre[9] que la vitesse de propagation dans l'eau en mouvement de l'expérience de Fizeau s'écrit donc :

$w_{+}={\frac {c/n+v}{1+v/nc}}$ ,

qui se développe au premier ordre lorsque v<<c/n en :

$w_{+}=c/n+v(1-1/n^{2})$

qui est très exactement la formule de l'entraînement partiel de Fresnel vu dans l'expérience de Fizeau. Avec l'aberration de la lumière en astronomie, cette expérience est donc l'une des confirmations expérimentales de la théorie de la relativité restreinte.

Références

Hippolyte Fizeau, « Recherches sur les modifications que subit la vitesse de la lumière dans le verre et plusieurs autres corps solides sous l’influence de la chaleur », Comptes-rendus de l'Académie des sciences, vol. 54,‎ 1862, p. 1237
« Interféromètre de Fizeau », sur Optique pour l'ingénieur (consulté le 30 octobre 2017)
(en) « Interféromètres laser », sur ZYGO (TM) (consulté le 30 octobre 2017)
(en) J.E. Greivenkam & J.H. Bruning, Phase Shifting Interferometry in Optical Shop Testing, D. Macalara, Wiley, 1992, p. 501-502
« Interférométrie et démodulation de franges », sur Optique pour l'ingénieur (consulté le 30 octobre 2017)
Hippolyte Fizeau, « Sur les hypothèses relatives à l'éther lumineux », Comptes Rendus de l'Académie des Sciences, vol. 33,‎ 1851, p. 349–355 (lire en ligne)
(en) Michelson, A. A., Morley, E.W., « Influence of Motion of the Medium on the Velocity of Light », American Journal of Science, vol. 31,‎ 1886, p. 377-386 (lire en ligne)
(en) Zeeman, Pieter, « Fresnel's coefficient for light of different colours », Proc. Kon. Acad. Van Weten, vol. 17,‎ 1914, p. 445–451
(de) Max von Laue, « Die Mitführung des Lichtes durch bewegte Körper nach dem Relativitätsprinzip », Annalen der Physik, vol. 328,‎ 1907, p. 989-990 (lire en ligne)

Voir aussi

Liens externes

Interféromètre de Fizeau
Réalisation d'un interféromètre de Fizeau pour la fabrication amateur d'optique d'astronomie

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.