Indicateurs de volume et de déplacement d'une structure architecturale

On entend par structure résistante toute chose, amorphe ou vivante, supportant sans se rompre les forces auxquelles elle peut normalement être soumise.

Caractérisée par sa forme et ses matériaux constitutifs, et tridimensionnelle par essence, la structure amorphe présente généralement une géométrie à deux dimensions, à laquelle on donne une épaisseur, ou une géométrie à trois dimensions (la structure tridimensionnelle). Cette dernière est formée de deux structures bidimensionnelles situées dans des plans non parallèles ou de volumes courbes tridimensionnels comme aussi pour toutes les choses vivantes dont une famille particulière concerne les coques (une surface tridimensionnelle avec une épaisseur), comme, par exemple, la structure des voitures, bateaux ou avions, ou encore des crânes humains, coquillages ou tiges de pissenlit.

La géométrie de la majorité des structures dites « architecturales » (telle que celles des bâtiments ou des ponts) est bidimensionnelle et son étude revêt une grande importance qu’il s’agisse d’esthétique, de commodité ou d’économie. De nombreux critères entrent donc en ligne de compte dans sa définition.

Ce travail se limite à la recherche de la géométrie conduisant à la structure de volume minimum.

Le coût d’une structure dépend de la nature et de la quantité des matériaux utilisés ainsi que des outils et des ressources humaines nécessaires à sa fabrication.

Si les progrès techniques permettent de réduire tant le coût des outils que l’importance des ressources humaines nécessaires, et si les outils de calcul informatique permettent maintenant de dimensionner une structure de manière qu’elle y soit sollicitée en tout point à la contrainte admissible de ses matériaux constitutifs, il faut aussi que sa géométrie soit optimale. La recherche de cet optimum est cependant loin d’être évidente, tant le choix est vaste.

En outre, la résistance de la structure n’est pas le seul critère à prendre en compte, il faut aussi dans de nombreux cas s’assurer du fait qu’elle ne se déforme pas de manière excessive sous charges statiques ou qu’elle ne se mette pas à vibrer de manière désagréable ou dangereuse sous charges dynamiques.

Cette approche ne tient pas compte des phénomènes d’instabilité élastique. Il peut en effet être démontré qu’il est toujours possible de dessiner la structure de manière à en rendre l’influence négligeable.

Il s’agit de dessiner la morphologie optimale pour une structure bidimensionnelle d’épaisseur constante :

• qui s’inscrit dans un rectangle de dimensions déterminées, longitudinale L et transversale H, exprimées en mètres (m) ;
• réalisée en un ou plusieurs matériaux présentant un(des) module(s) d’élasticité E, exprimée en pascal (Pa), et sollicité(s) en tout point à sa (ses) contrainte(s) admissible(s) σ, exprimée (en Pa) ;
• résistante aux sollicitations maximales auxquelles elle est soumise, sous la forme d’une « résultante » F, exprimée en newtons (N).

À chaque forme choisie correspond un volume de matière V (en mètres cubes) et une déformation maximale δ (en mètres).

Leur calcul dépend des facteurs L, H, E, σ, et F. Ces calculs sont longs et fastidieux, ils  brouillent la recherche de la forme optimale.

Il est cependant possible de s’affranchir de ces facteurs en les portant à l’unité, toute autre caractéristique restant égale. La longueur L est ainsi ramenée à 1 m, H à H/L, E et σ à 1 Pa, et F à 1N.

À cette structure « réduite » correspond un volume de matière W= σV/ FL (l’indicateur de volume) et une déformation maximale Δ = Eδ / σL (l’indicateur de déplacement).

Ils ont pour principale caractéristique d’être des nombres sans dimensions physiques (adimensionnels) et dont la valeur, pour chaque morphologie considérée, ne dépend que du rapport L/H, c’est-à-dire de l’élancement géométrique de la forme.

La méthode s’étend aisément aux structures tridimensionnelles comme illustré dans les exemples qui suivent.

La théorie relative aux indicateurs est enseignée depuis 2000, entre autres, au département du génie civil et d’architecture de la Vrije Universiteit Brussel (VUB : service de mécanique des matériaux et des constructions), et y a fait l’objet de recherches et contributions régulières sous la direction de D^r Ir Philippe Samyn (de 2000 à 2006), de D^r Ir Willy Patrick De Wilde (de 2000 à 2011) et de D^r Ir Lincy Pyl maintenant.

L’ouvrage de référence[1], depuis la thèse en référence[2], rend compte du développement de la théorie chez Samyn and Partners et à la VUB jusqu’en 2004.

La théorie est ouverte à qui veut contribuer car W et Δ peut se calculer pour n’importe quelle structure résistante telle que définie ci-dessus.

Les progrès en sciences des matériaux, en robotique et en impression tridimensionnelle permettent de créer de nouvelles formes structurelles plus légères que les plus légères connues à ce jour. C’est ainsi, et par exemple, que la géométrie des surfaces minimales en un matériau homogène d’épaisseur constant est fortement modifiée par la variation tant de l’épaisseur que de la résistance locale du matériau.

Les macrostructures étudiées ici peuvent être composées « d’éléments structurels » dont le matériau présente une « microstructure ».

Que l'on cherche à limiter la contrainte ou la déformation, macrostructure, élément structurel et microstructure ont chacun un poids Vρ, où ρ est le poids volumique des matériaux, en N/m³, qui est fonction des sollicitations {F₀} (pour « force » en général) qui leur sont appliquées, de leur taille {L₀} (pour « taille » en général) , de leur forme {G_e} (pour « forme » en général), de la matière qui les constituent {M_a} (pour « matière » en général).

${\displaystyle V\rho \div \left\{F_{0}\right\}\left\{L_{0}\right\}\left\{G_{e}\right\}\left\{M_{a}\right\}}$

Ou encore, forme et matière ({G_e}{M_a}) définissent le poids (Vρ) de la structure répondant aux sollicitations et aux portées voulues ({F₀}{L₀}).

${\displaystyle {\frac {V\rho }{\left\{F_{0}\right\}\left\{L_{0}\right\}}}\div \left\{G_{e}\right\}\left\{M_{a}\right\}}$

En mécanique des matériaux et au niveau de l’élément structurel, le paramètre {G_e} correspond, pour un type de sollicitations considéré, au «facteur de forme» pour les structures de section continue en matériau ne comportant pas de vides.

Le matériau constitutif de l’élément structurel peut cependant posséder une microstructure telle qu’il comprend des vides. Il a alors une structure cellulaire qui améliore dans tous les cas de charge le facteur de forme.

Le paramètre {M_a} caractérise le matériau et permet d’en comparer l’efficacité par rapport à un autre pour un type de sollicitations donné, et ce indépendamment du «facteur de forme» de la structure, caractérisé par {G_e}.

Les indicateurs W = σV/FL et Δ = δE/σL qui viennent d’être définis caractérisent les macrostructures, alors que les mêmes notations et symboles en minuscule renverront toujours à l’élément structurel. Ainsi, w = σv/fl et Δ = δE/σl sont les indicateurs de volume et de déplacement de l’élément structurel.

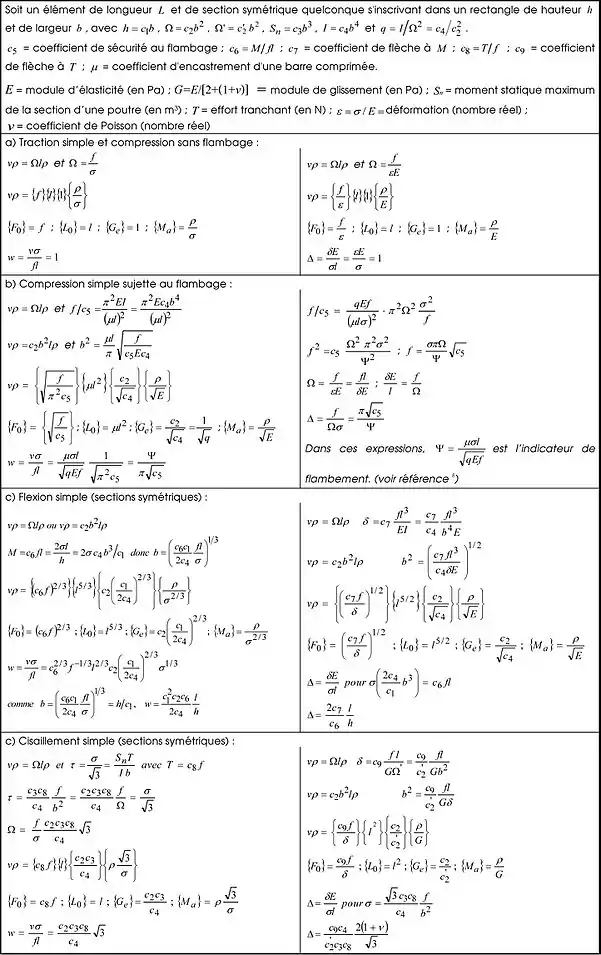
La figure 1 reprend, au niveau de l’élément structurel, les formulations de Vρ ainsi que de W et Δ pour la traction, la compression, la flexion et le cisaillement simple. La colonne de gauche concerne la limitation des contraintes, celle de droite la limitation des déformations.

L’indicateur W est, comme on peut l’observer, en relation directe avec {G_e}{M_a}. En effet :

${\displaystyle V\rho \div \left\{F_{0}\right\}\left\{L_{0}\right\}\left\{G_{e}\right\}\left\{M_{a}\right\}\div V\sigma \cdot \rho /\sigma }$, d'où ${\displaystyle V\sigma \div \left\{F_{0}\right\}\left\{L_{0}\right\}\left\{G_{e}\right\}\left\{M_{a}\right\}\cdot \sigma /\rho .}$
ou: ${\displaystyle W={\frac {\sigma V}{FL}}\div \left[{\frac {\left\{F_{0}\right\}}{F}}\right]\left[{\frac {\left\{L_{0}\right\}}{L}}\right]\left\{G_{e}\right\}\left\{M_{a}\right\}{\frac {\sigma }{\rho }}}$.
ou encore: ${\displaystyle W\div \left\{G_{e}\right\}\left\{M_{a}\right\}\sigma /\rho \ }$ pour un état de sollicitation et une dimension donnés.
Dans ce cas, comme W et Δ ne dépendent que de ${\displaystyle L/H\ }$ :
${\displaystyle W={\frac {\sigma V}{FL}}={\frac {\rho V}{FL}}{\frac {\sigma }{\rho }}\ }$ et donc : ${\displaystyle W{\frac {\rho }{\sigma }}={\frac {\rho V}{FL}}\div \left\{G_{e}\right\}\left\{M_{a}\right\}.}$

Pour un type de sollicitation considéré, il s’agit donc du poids spécifique d’une macrostructure par unité de force et de longueur, qui ne dépend de la géométrie que par l’intermédiaire de L/H, et des matériaux que par l’intermédiaire de σ/ρ .

Wρ/σ intègre donc, sans les révéler, l’indice {M_a} d’efficience des matériaux (ρ/σ et ρ/E pour la traction et la compression hors flambage, ρ/E^1/2 pour la compression limitée par le flambage, ρ/σ^2/3 et ρ/E^1/2 pour la flexion simple, ρ√3 /σ et ρ/G pour le cisaillement) et l’indice d’efficience {G_e} de la forme.

Toutes autres choses restant égales, une grappe de tubes de diamètre H et d’épaisseur de paroi e remplaçant une barre pleine de même volume en un matériau aux caractéristiques physiques ρ , σ , E et G , présente une densité apparente ρ_a = 4k(1-k)ρ où k=e/H , une contrainte admissible apparente σ_a = 4k(1-k)σ, un module d’élasticité apparent E_a = 4k(1-k)E et un module de glissement apparent G_a = 4k(1-k)G. Il en découle que

${\displaystyle \rho _{a}/E_{a}^{1/2}=2{\sqrt {k-k^{2}}}\rho /E^{1/2}\ }$ et ${\displaystyle \rho _{a}/\sigma _{a}^{2/3}=(4k-4k^{2})^{1/3}\rho /\sigma ^{2/3}}$

Ceci explique les meilleures performances des matériaux allégés pour les éléments structurels en compression et sujets à flambement, ainsi que pour les éléments fléchis.

Cet indicateur permet donc de comparer l’efficience de macrostructures ou de systèmes intégrés différents comprenant géométrie et matériau.

La présente approche morphologique fait écho aux travaux de M.F. Ashby qui s'attache, dans son ouvrage Materials Selection in Mechanical Design (1992)[3], à définir une méthode de sélection de matériaux. {G_e} et {M_a} y sont analysés séparément car, pour ses études, {M_a} doit couvrir un grand nombre de caractéristiques physiques des matériaux.

Différente et complémentaire, elle peut également être mise en parallèle avec les travaux menés à partir de 1969 par l'Institut für leichte flächentragwerke à Stuttgart sous la direction de Frei Otto puis de Werner Sobek, qui font référence à des indices nommés Tra et Bic[4]. Le Tra est défini comme le produit de la longueur de la trajectoire de la force F_r, (menant la structure à la ruine) vers les appuis par l'intensité de cette force, et le Bic est le rapport de la masse de la structure au Tra.

ρ* étant la masse volumique du matériau (en kg/m³), et α étant, comme W, une constante dépendant du type de structure et du cas de charge :

${\displaystyle Bic=\rho ^{*}V/Tra\ }$ et ${\displaystyle \ Tra=F_{r}L/\alpha \ }$ ; donc, avec la contrainte à la rupture ${\displaystyle \sigma _{r}}$ atteinte sous ${\displaystyle F_{r}}$
${\displaystyle Bic=\alpha {\frac {\rho ^{*}V}{F_{r}L}}=\alpha {\frac {\rho ^{*}}{\sigma }}{\frac {F}{F_{r}}}W\ }$ ; et comme ${\displaystyle \ {\frac {F}{F_{r}}}={\frac {\sigma }{\sigma _{r}}}\$ :\ Bic={\frac {\rho ^{*}}{\sigma _{r}}}\alpha W} .

Contrairement à W, qui est sans dimensions, Bic s'exprime en kg/Nm. Dépendant donc du matériau, il ne permet pas une comparaison indépendante de différentes morphologies.

Il est étonnant de remarquer que malgré l'abondance de leur travaux, aucun n'ait mis en évidence ni ne se soit attaché à étudier W et sa relation avec L/H.

Il semble que seuls V. Quintas Ripoll[5] - [6] et W. Zalewski et St. Kus[7] aient approché l’indicateur de volume W sans toutefois approfondir la question.

Figure1 : Les indicateurs de volume W = σv / fl et de déplacement Δ = δE/σl de l’élément structurel.

Les effets de second ordre n'ont en général que très peu d'influence sur W, alors qu'ils peuvent sensiblement influencer Δ. W et Δ dépendent alors aussi de E/σ.

L'effort tranchant T peut être déterminant dans le cas de pièces fléchies, courtes et continues, soumises à flexion de telle sorte que W ne descende plus en-dessous d'une certaine valeur, quelle que soit la réduction de l'élancement L/H. Cette limitation est cependant très théorique car il est toujours possible de la supprimer en transférant de la matière des ailes vers la (ou les) âme(s) près des appuis.

La contrainte σ à laquelle la structure peut être sollicitée dépend de la nature, de la géométrie interne, du mode de production et de mise en œuvre des matériaux, ainsi que de nombreux autres facteurs tels que la précision dimensionnelle de la construction réelle, la nature des assemblages des éléments ou la résistance au feu, mais également de l'habileté avec laquelle la géométrie de la structure est définie pour se prémunir des phénomènes d'instabilité élastique. Pierre Latteur[8], qui a découvert l’indicateur de flambement a étudié l’influence des phénomènes d’instabilité élastique sur W et Δ. Il est à ce sujet important de noter que les contingences d'ancrage d'un élément en traction peuvent en réduire la contrainte admissible apparente au même niveau que la réduction nécessaire pour tenir compte d'une instabilité élastique modérée. L’influence sur W du flambage des pièces comprimées d’une part et des ancrages aux extrémités de pièces tendues d’autre part, est analysée pp. 30 à 58 dans l'"ouvrage de référence"[1].

La contrainte de travail σ est aussi souvent réduite par la nécessité de limiter le déplacement δ de la structure puisqu'il n'est pas possible de beaucoup faire varier E pour un matériau donné.

Les considérations relatives à la fatigue, à la ductilité et aux efforts dynamiques viennent également limiter la contrainte de travail admissible.

Il n'est pas toujours aisé de fixer la nature et l'intensité maximale totale des forces F (y compris le poids propre) à laquelle la structure est soumise, ce qui influence à nouveau directement les contraintes de travail.

Les assemblages des éléments comprimés ou tendus sont considérés comme articulés. Tout encastrement, même partiel, induit un moment parasite qui a pour conséquence d'alourdir la structure.

Le volume des assemblages vient finalement, pour certains types de structures, s'ajouter au volume net défini par W. Son importance dépend de la nature du matériau et du contexte ; elle est à déterminer dans chaque cas.

Il s'ensuit que n'entrent principalement en ligne de compte que W et Δ pour la conception morphologique d'une structure, en acceptant qu'elle soit hyperamortie (c'est-à-dire que son amortissement interne soit supérieur à l'amortissement critique), ce qui la rend insensible aux sollicitations dynamiques.

Le volume V d'une structure est donc directement proportionnel à l'intensité totale de la force F qui y est appliquée, à sa longueur L et au facteur morphologique W; il est inversement proportionnel à la contrainte σ à laquelle il peut être sollicité. Le poids d'une structure est en outre proportionnel à la densité ρ de son matériau constitutif. Par contre, son déplacement maximum δ reste proportionnel à la portée L et au facteur morphologique Δ, ainsi qu'au rapport de sa contrainte de travail σ au module d'élasticité E.

S'il consiste à limiter le poids (ou le volume) et la déformation d'une structure pour un état de sollicitation F et une portée L donnés, toutes autres considérations restant égales, l'art de l'ingénieur en structures consiste donc à minimaliser W et ρ/σ d'une part et Δ et σ/E d'autre part.

Les figures suivantes précisent les valeurs des indicateurs en fonction de L/H pour quelques types de structures.

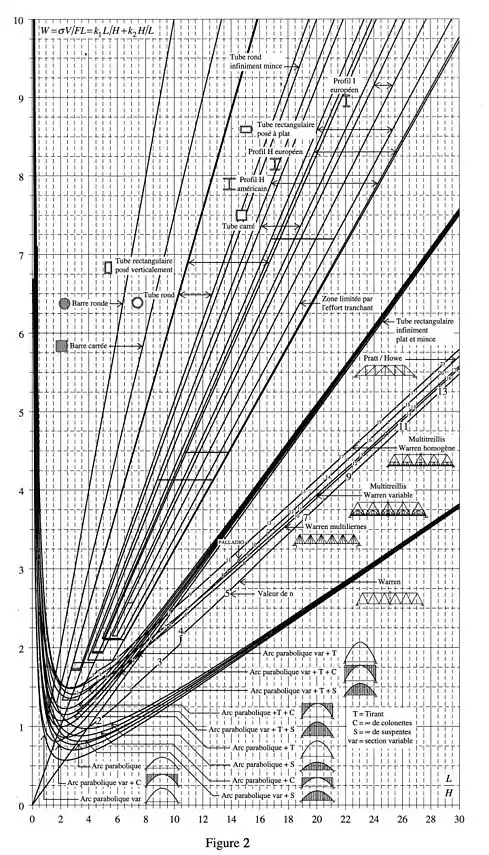
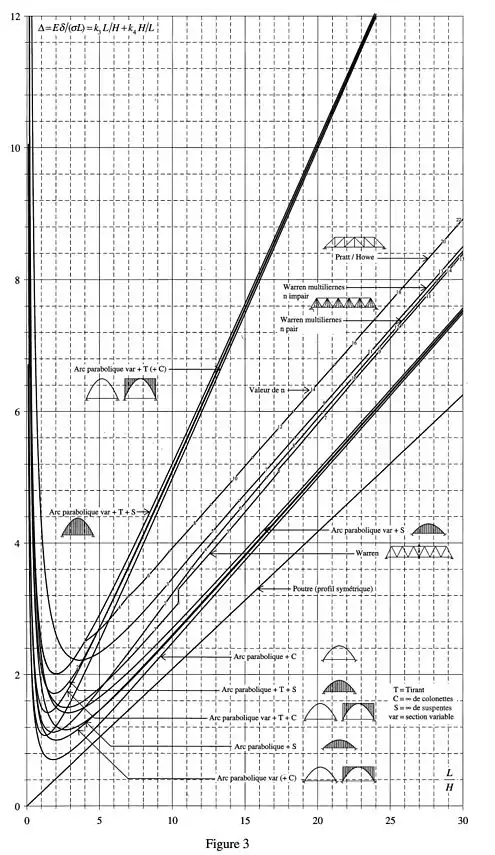
Figure 2 et 3 : W et Δ pour une portée horizontale isostatique sous une charge verticale uniformément répartie réalisée en :

• profils de section constante, du cylindre plein au I ;
• treillis de différents types ;
• arcs paraboliques avec/sans suspentes ou colonnettes, de section constante ou variable.

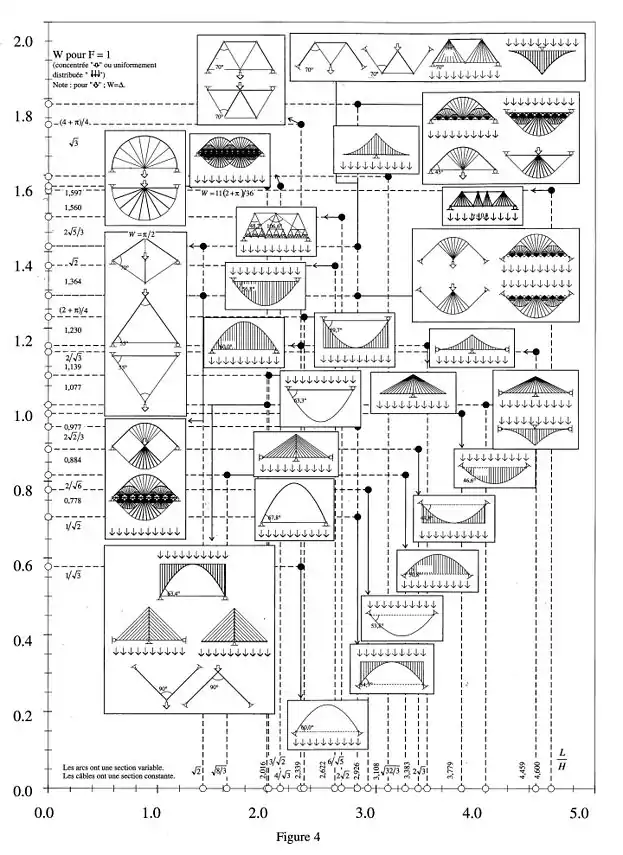
Figure 4 : W pour le transfert vers deux appuis équidistants sur l’horizontale d’une charge verticale F=1, ponctuelle (dans ce cas Δ= W) ou uniformément répartie.

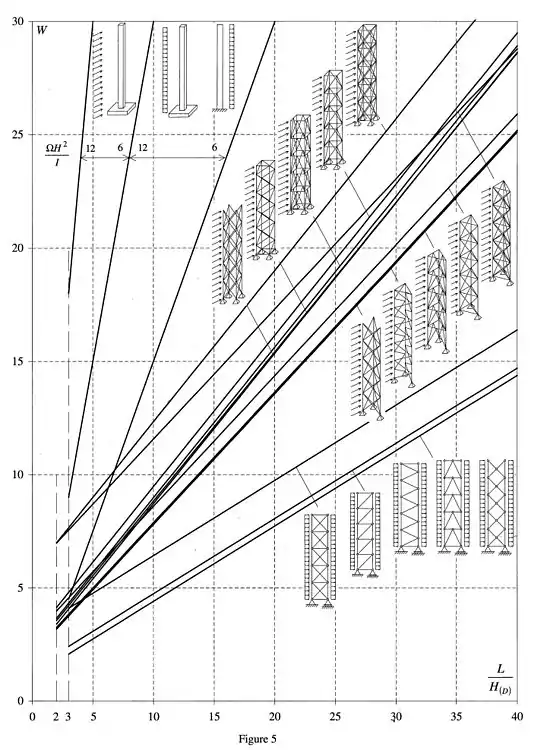
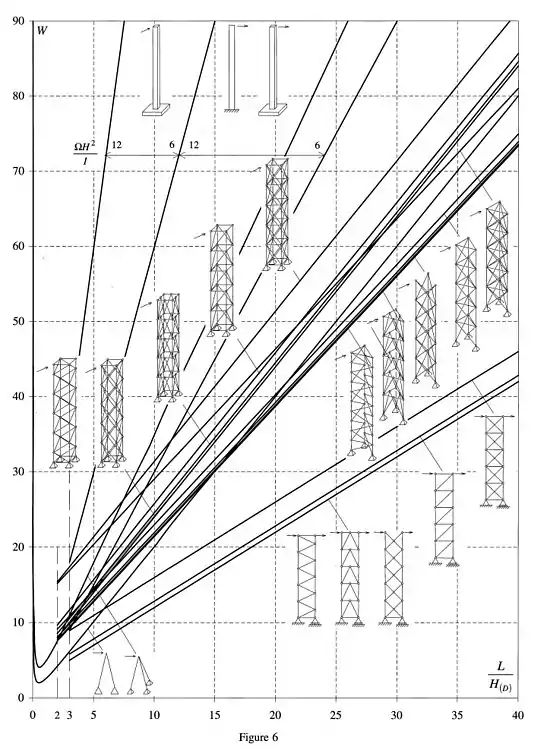
Figure 5 et 6 : W pour un mât vertical, de largeur constante, soumis à une charge horizontale uniformément répartie sur sa hauteur ou concentrée en tête.

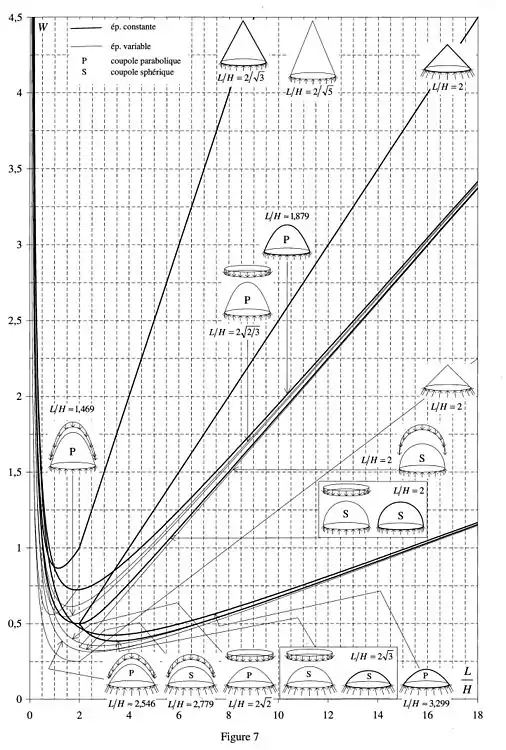
Figure 7 : W pour une coupole de révolution à axe vertical en membrane, d’épaisseur constante ou variable, sous charge uniformément répartie verticale. Il est étonnant de constater que la valeur minimale est atteinte pour une coupole cônique d’épaisseur variable avec un angle d’ouverture de 90° (L/H= 2 ; W= 0,5 !).

• les treillis,
• la poutre droite continue,
• l’arc, le câble et la structure haubanée,
• les mâts,
• les portiques,
• la coupole de révolution en membrane.

W peut aisément être déterminé pour optimiser des structures composées de plusieurs éléments constructifs différents (voir l'"ouvrage de référence"[1];pp. 100-106) tel que par exemple pour le mât d’éolienne illustré en figure 8.

Figure 8

ou une couverture en arc parabolique couplée avec de larges tympans vitrés soumis au vent telle que celle de la gare de Leuven en Belgique illustré en figure 9 (voir référence[11] pour analyse détaillée).

Figure 9

L'optimisation de la structure en trellis de la façade du bâtiment Europa à Bruxelles (voir référence[12] pp. 93-101 pour l'analyse détaillée) est un autre exemple.

Figure 10