Inégalité de Young

L'inégalité de Young peut être utilisée dans la preuve de l'inégalité de Hölder. Elle est également largement utilisée pour estimer la norme de termes non linéaires en théorie des équations aux dérivées partielles, puisqu'elle permet d'estimer un produit de deux termes par une somme des deux mêmes termes à une puissance quelconque et divisé par un nombre.

L'aire du rectangle (ab) ne peut dépasser la somme des aires correspondant à l'intégrale de la fonction ${\displaystyle f}$ (en rouge) et de la fonction ${\displaystyle f^{-1}}$ (en jaune).

L'inégalité ci-dessus est un cas particulier de la suivante, démontrée par Young[2] :

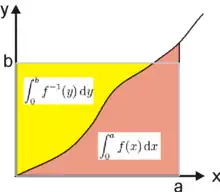
Soit ${\displaystyle f}$ une fonction continue strictement croissante sur ${\displaystyle [0,c]}$ (avec ${\displaystyle c>0}$) et ${\displaystyle f^{-1}}$ sa bijection réciproque. Si ${\displaystyle f(0)=0}$, ${\displaystyle a\in [0,c]}$ et ${\displaystyle b\in [0,f(c)]}$ alors

${\displaystyle ab\leq \int _{0}^{a}f(x)\,\mathrm {d} x+\int _{0}^{b}f^{-1}(y)\,\mathrm {d} y}$,

avec égalité si et seulement si ${\displaystyle b=f(a)}$[3].

Le diagramme ci-contre donne une preuve graphique très simple de ce résultat, en interprétant les deux intégrales comme deux aires bordées par le graphe de ${\displaystyle f}$.

Le calcul précédent revient à dire que si F est une fonction strictement convexe de classe C¹ alors, en notant G sa transformée de Legendre (ou fonction conjuguée)[4],

${\displaystyle ab\leq F(a)+G(b).}$

Sous cette forme, cette inégalité est encore valide si F est une fonction convexe à argument vectoriel[5].

Pour des details, Mitroi&Niculescu [6].

Exemples

• La transformée de Legendre de F(a) = a^p/p est G(b) = b^q/q avec q tel que 1/p + 1/q = 1, et ainsi l'inégalité de Young standard est un cas particulier[7].
• La transformée de Legendre de F(a) = e^a est G(b) = b ln b – b, et alors ab ≤ e^a + b ln b – b pour tous a et b positifs ou nuls.