Inégalité de Bernoulli
En analyse, l'inégalité de Bernoulli — nommée d'après Jacques Bernoulli — énonce que :
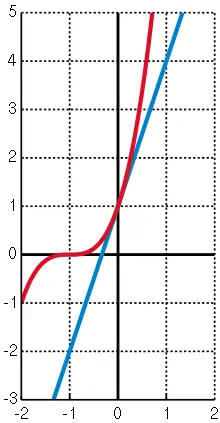
Illustration de l'inégalité de Bernoulli pour
pour tout entier[1] n > 1 et tout réel x non nul supérieur ou égal à −1.
Démonstration par récurrence
Soit un réel . Montrons l'inégalité pour tout entier n > 1, par récurrence[2] sur n.
- Initialisation : donc la propriété est vraie pour n = 2.
- Hérédité : supposons (hypothèse de récurrence) que et montrons que la propriété est vraie au rang suivant k + 1, c'est-à-dire montrons que .
En multipliant les deux membres de l'inégalité de l'hypothèse de récurrence par 1 + x (qui par hypothèse est positif ou nul) on obtient : . - Conclusion : la propriété est vraie au rang 2 et elle est héréditaire donc vraie pour tout entier n ≥ 2.
Généralisation
Pour tout réel r > 1 et tout réel x non nul et supérieur ou égal à −1, on a encore :
Utilisations
L'inégalité de Bernoulli peut être utilisée comme lemme pour démontrer que pour tout réel q > 1, la limite de la suite géométrique (qn) est +∞.
Notes et références
- (en) Visualisation par une animation interactive, sur demonstrations.wolfram.com
- Une méthode plus rapide est d'utiliser la formule du binôme si x > 0 ((en) Eric W. Weisstein, « Bernoulli Inequality », sur MathWorld) et la formule de la somme des premiers termes d'une suite géométrique si −1 ≤ x < 0 ().
Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.


![{\displaystyle x\in \left[-1,0\right[\cup \left]0,+\infty \right[}](https://img.franco.wiki/i/f74f7e6f1481529c88df2c73ed703f8cd271be52.svg)









![{\displaystyle \left[-1,0\right[\cup \left]0,+\infty \right[}](https://img.franco.wiki/i/fd538abd3c3db58bfea6a6623f82971cfc9d4c43.svg)
