Impulsion (signal)
Dans le domaine du traitement de signal, une impulsion est un changement rapide et transitoire de l'amplitude d'un signal d'une valeur de base à une valeur supérieure ou inférieure, suivi d'un retour rapide à la valeur de base[1].
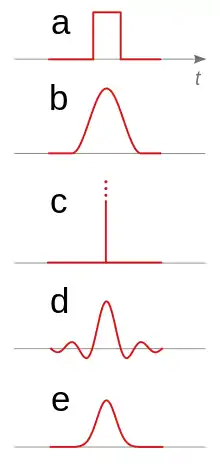
(b) impulsion cosinus carré (cosinus surélevé),
(c) impulsion de Dirac,
(d) impulsion sinc,
(e) impulsion gaussienne.
Formes d'impulsion
Les impulsions peuvent prendre différente formes. Celles-ci peuvent résulter d'un processus de mise en forme d'impulsion (en).
Impulsions rectangulaires
Les impulsions rectangulaires (en) suivent une fonction porte. Dans les signaux numériques, les transitions montante et descendante entre les niveaux haut et bas sont appelées flancs montant et descendant.
Impulsions Nyquist
Une impulsion Nyquist est une impulsion qui répond au critère Nyquist ISI (en). Elle possède une certaine importance dans le domaine de la transmission de données. Un exemple d'impulsion qui remplit cette condition est la fonction sinus cardinal (sinc).
En 2013, des impulsions Nyquist ont été produites dans le but de réduire la taille des impulsions dans les fibres optiques. Celles-ci ont pu être entassées 10 fois plus étroitement les unes contre les autres, ce qui entraîne une augmentation correspondante de 10 fois de la bande passante[2] - [3].
Impulsions gaussiennes
Une impulsion gaussienne a la forme d'une fonction gaussienne et est produite par un filtre gaussien. Elle possède une pente de transition maximale sans dépassement ainsi qu'un un retard de groupe minimal.
Notes et références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Pulse (signal processing) » (voir la liste des auteurs).
- (en)Ángela Molina, Joaquín González, Pulse Voltammetry in Physical Electrochemistry and Electroanalysis, Springer, 2015 (ISBN 3319212516).
- (en) Joel Detrow, « Pointy pulses improve optical fiber throughput by a factor of 10 », Gizmag.com (consulté le )
- (en) Marcelo A. Soto, Mehdi Alem, Mohammad Amin Shoaie et Armand Vedadi, « Optical sinc-shaped Nyquist pulses of exceptional quality : Nature Communications : Nature Publishing Group », Nature.com (consulté le )