Hinfini

La synthèse H_∞ est une méthode qui sert à la conception de commandes optimales. Il s'agit essentiellement d'une méthode d'optimisation, qui prend en compte une définition mathématique des contraintes en ce qui concerne le comportement attendu en boucle fermée. La commande Hinfini a pour principal avantage la capacité d'inclure dans un même effort de synthétisation les concepts liés à la commande classique et à la commande robuste.

Le mot « optimal » est utilisé dans son sens strictement mathématique car la commande synthétisée est celle qui minimisera l'effet des entrées/sorties du système, ce qui peut être vu comme "non optimal" par les opérateurs (l'optimisation étant relative à l'objectif recherché).

Le « infini » dans Hinfini signifie que ce type de commande est conçu pour imposer des restrictions de type minimax au sens de la théorie de la décision (minimiser la perte maximale possible) dans le domaine fréquentiel. La norme Hinfini d'un système dynamique est l'amplification maximale que le système peut exercer sur l'énergie du signal d'entrée. Dans le cas d'un système MIMO, ceci équivaut au maximum de la plus grande valeur singulière du système, ce qui, dans le cas SISO, se traduit par la valeur maximale de l'amplitude de sa réponse fréquentielle.

Considérant le système représenté par la forme standard suivante:

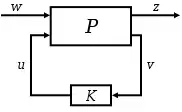
Le système P possède deux entrées:

• w représente les entrées extérieures, notamment le vecteur de consigne de commande, les perturbations et les bruits,
• u représente le vecteur de commande ;

et deux sorties :

• z les sorties à optimiser pour avoir un bon comportement de la commande
• v les mesures disponibles utilisées par le contrôleur pour calculer la commande.

Toutes ces données sont d’une façon générale des vecteurs et P et K sont des matrices.

Le système précédent peut s’écrire sous la forme:

${\displaystyle {\begin{bmatrix}z\\v\end{bmatrix}}=\mathbf {P} (s)\,{\begin{bmatrix}w\\u\end{bmatrix}}={\begin{bmatrix}P_{11}(s)&P_{12}(s)\\P_{21}(s)&P_{22}(s)\end{bmatrix}}\,{\begin{bmatrix}w\\u\end{bmatrix}}}$

${\displaystyle u=\mathbf {K} (s)\,v}$

Il est alors possible d’exprimer la relation entre z et w par:

${\displaystyle z=F_{\ell }(\mathbf {P} ,\mathbf {K} )\,w}$

Où ${\displaystyle F_{\ell }}$ est appelé la ‘’Transformation Linéaire Fractionnaire’’ (LFT) définie par:

${\displaystyle F_{\ell }(\mathbf {P} ,\mathbf {K} )=P_{11}+P_{12}\,\mathbf {K} \,(I-P_{22}\,\mathbf {K} )^{-1}\,P_{21}}$

L’objectif de la synthèse ${\displaystyle {\mathcal {H}}_{\infty }}$ est de trouver le contrôleur ${\displaystyle \mathbf {K} }$ tel que la norme ${\displaystyle {\mathcal {H}}_{\infty }}$ de ${\displaystyle F_{\ell }(\mathbf {P} ,\mathbf {K} )}$ soit minimum. La norme ${\displaystyle {\mathcal {H}}_{\infty }}$ de la matrice de fonctions de transfert ${\displaystyle F_{\ell }(\mathbf {P} ,\mathbf {K} )}$ est définie par:

${\displaystyle ||F_{\ell }(\mathbf {P} ,\mathbf {K} )||_{\infty }=\sup _{\omega }{\bar {\sigma }}(F_{\ell }(\mathbf {P} ,\mathbf {K} )(j\omega ))}$

où ${\displaystyle {\bar {\sigma }}}$ est la valeur singulière maximale de la matrice ${\displaystyle F_{\ell }(\mathbf {P} ,\mathbf {K} )(j\omega )}$.

Il existe plusieurs méthodes permettant le calcul et l’optimisation de la norme ${\displaystyle {\mathcal {H}}_{\infty }}$ :

• méthode basée sur la résolution des équations de Riccati ;
• méthode(s) basée sur les Inégalités matricielles linéaires ;
• méthode utilisant la paramétrisation de Youla.

La synthèse de commande ${\displaystyle {\mathcal {H}}_{\infty }}$ est depuis le début des années 2000 utilisée dans le cadre du contrôle de structures flexibles des systèmes spatiaux comme les satellites [1] ou les lanceurs[2]. Ces systèmes possèdent des modes de flexions proches de la bande passante du contrôleur et dont les caractéristiques sont incertaines (fréquence, gain, amortissement). La méthode ${\displaystyle {\mathcal {H}}_{\infty }}$ permet de garantir théoriquement une certaine robustesse de la stabilité du système (via la marge de module) tout en assurant les performances de réjection de perturbation.

Sur Ariane 5, le pilotage basé ${\displaystyle {\mathcal {H}}_{\infty }}$ a ainsi permis de garantir la stabilité du lanceur tout en optimisant la commande de braquage de la tuyère, faisant économiser plusieurs centaines de kilos sur le liquide hydraulique de commande[3].

• Commande LQ
• Commande LQG
• Commande optimale