Graphe partitionnable

Soit ${\displaystyle n}$ un entier strictement positif, une partition de ${\displaystyle n}$ est une suite d’entiers ${\displaystyle (s_{1},\ldots ,s_{m})}$ telle que :

• ${\displaystyle m\geq 1}$
• ${\displaystyle \forall i\in \left\{1,...,m\right\},s_{i}>0}$
• ${\displaystyle s_{1}+\ldots +s_{m}=n}$

Une ${\displaystyle k}$-partition de ${\displaystyle n}$ est une partition de ${\displaystyle n}$ possédant ${\displaystyle k}$ éléments.

Soit ${\displaystyle G=(V,E)}$ un graphe simple où :

• ${\displaystyle V}$ est l'ensemble non vide des sommets de G.
• ${\displaystyle E}$ est l'ensemble des arêtes de G, c'est-à-dire un sous-ensemble de l'ensemble des parties à deux éléments de ${\displaystyle V}$.

Soit ${\displaystyle S=(s_{1},\ldots ,s_{m})}$ une partition de ${\displaystyle |V|}$ (le nombre de sommets du graphe G).

${\displaystyle G}$ est dit admettre une ${\displaystyle S}$-partition s'il existe une partition ${\displaystyle P(S)=\left\{V_{i}:i\in \left\{1,...,m\right\}\right\}}$ de ${\displaystyle V}$ telle que :

• ${\displaystyle \forall i\in \left\{1,...,m\right\},|V_{i}|=s_{i}}$
• ${\displaystyle \forall i\in \left\{1,...,m\right\},G[V_{i}]}$ est un graphe connexe.

L'ensemble ${\displaystyle P(S)}$ est alors dit être une partition de ${\displaystyle G}$ induite par ${\displaystyle S}$.

Un graphe ${\displaystyle G=(V,E)}$ est dit partitionnable s'il admet une ${\displaystyle S}$-partition pour toute partition ${\displaystyle S}$ de ${\displaystyle |V|}$.

Un graphe ${\displaystyle G}$ est dit ${\displaystyle k}$-partitionnable s'il admet une ${\displaystyle S}$-partition pour toute ${\displaystyle k}$-partition ${\displaystyle S}$ de ${\displaystyle |V|}$.

• Une ${\displaystyle 2}$-partition de ${\displaystyle 5}$ est ${\displaystyle (3,2)}$.
• Une ${\displaystyle 4}$-partition de ${\displaystyle 10}$ est ${\displaystyle (1,4,1,4)}$.
• Une ${\displaystyle 7}$-partition de ${\displaystyle 22}$ est ${\displaystyle (2,2,3,1,3,8,3)}$.

Soit le graphe ${\displaystyle G=(V,E)}$ tel que :

• ${\displaystyle V=\left\{a,b,c,d,e,f\right\}}$
• ${\displaystyle E=\left\{\left\{a,b\right\},\left\{b,c\right\},\left\{c,d\right\},\left\{d,e\right\},\left\{e,f\right\},\left\{f,a\right\},\left\{c,e\right\}\right\}}$

représenté ci-dessous par :

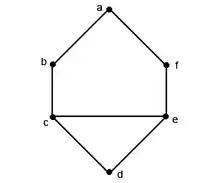
${\displaystyle |V|=6}$. ${\displaystyle G}$ admet 3 partitions de 6 possibles : ${\displaystyle (1,1,4)}$, ${\displaystyle (1,2,3)}$ et ${\displaystyle (2,2,2)}$ (en considérant que l'ordre des différentes suites n'a pas d'importance).

Ces trois partitions de l'entier 6 peuvent être appliquées respectivement pour partager le graphe ${\displaystyle G}$ comme ceci :

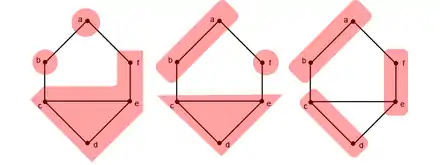
Il existe bien d'autres façons d'appliquer ces 3 partitions sur ce graphe. Le schéma ci-dessus est une des représentations possibles.