Graphe de Mycielski

Le graphe de Grötzsch ${\displaystyle M_{4}}$ construit comme le mycielkien du graphe-cycle à 5 sommets M_3

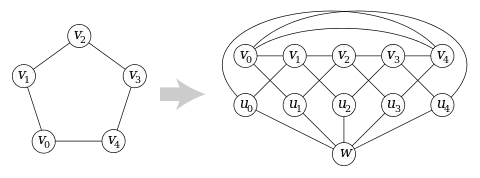
Soit ${\displaystyle G=(V,E)}$ un graphe. Le mycielkien de ce graphe noté ${\displaystyle M(G)}$ est le graphe ${\displaystyle (V_{M},E_{M})}$ avec ${\displaystyle V_{M}=V\cup V'\cup \{u\}}$ où ${\displaystyle V'}$ est une copie de ${\displaystyle V}$ et ${\displaystyle E_{M}=E\cup E'\cup E''}$ où ${\displaystyle E'=\{\{u,v'\}|v'\in V'\}}$ et ${\displaystyle E''=\{\{v_{i},v_{j}'\}|v_{i}\in V,v_{j}'\in V',\{v_{i},v_{j}\}\in E\}}$.

Les graphes de Mycielski sont les graphes ${\displaystyle M_{n}}$ définis par la récurrence suivante : ${\displaystyle M_{2}}$ est le graphe à une arête, et ${\displaystyle M_{n+1}=M(M_{n})}$.

Graphes de Mycielski M₂, M₃ et M₄

• Si le nombre chromatique de G est k, alors celui de M(G) est k+1[1].
• Si G est sans triangle, alors M(G) aussi[1].
• Si G possède un cycle hamiltonien, alors M(G) aussi[2].
• Si le nombre de domination de G est γ(G), alors celui de M(G) est γ(G)+1[2].

• (en) Valerie King, « A Simpler Minimum Spanning Tree Verification Algorithm », Algorithmica, vol. 18, n^o 2,‎ 1997, p. 263-270

• (en) Vašek Chvátal, « The minimality of the Mycielski graph », Graphs and Combinatorics (Proc. Capital Conf., George Washington Univ., Washington, D.C., 1973),‎ 1974
• (en) Tomislav Došlić, « Mycielskians and matchings », Discussiones Mathematicae Graph Theory, vol. 25,‎ 2005.
• (en) David C. Fisher, Patricia A. McKenna et Elizabeth D. Boyer, « Hamiltonicity, diameter, domination, packing, and biclique partitions of Mycielski's graphs », Discrete Applied Mathematics, vol. 84,‎ 1998, p. 93–105 (DOI 10.1016/S0166-218X(97)00126-1).
• Wensong Lin, Jianzhuan Wu, Peter Che Bor Lam et Guohua Gu, « Several parameters of generalized Mycielskians », Discrete Applied Mathematics, vol. 154, n^o 8,‎ 2006, p. 1173–1182 (DOI 10.1016/j.dam.2005.11.001).
• Jan Mycielski, « Sur le coloriage des graphes », Colloq. Math., vol. 3,‎ 1955, p. 161–162 (lire en ligne).
• C. Tardif, « Fractional chromatic numbers of cones over graphs », Journal of Graph Theory, vol. 38, n^o 2,‎ 2001, p. 87–94 (DOI 10.1002/jgt.1025).

• (en) Eric W. Weisstein, « Graphe de Mycielski », sur MathWorld