Graphe d'Andrásfai
En théorie des graphes, un graphe d'Andrásfai est un graphe circulant sans triangle ; il porte le nom de Béla Andrásfai[1] .
| Graphe d'Andrásfai | |
.svg.png.webp)
| |
| Notation | And(n) |
|---|---|
| Nombre de sommets | |
| Diamètre | 2 (pour n>1) |
| Propriétés | graphe circulant sans triangle |
.jpg.webp)
Définition
Pour tout entier naturel , le graphe d'Andrásfai d'ordre n , noté And(n) est un graphe circulant sur sommets, dans lequel tout sommet est reliée par une arête aux sommets pour tout entier congru à 1 mod 3. Par exemple, le graphe de Wagner est un graphe d'Andrásfai : c'est le graphe And (3).
Exemples
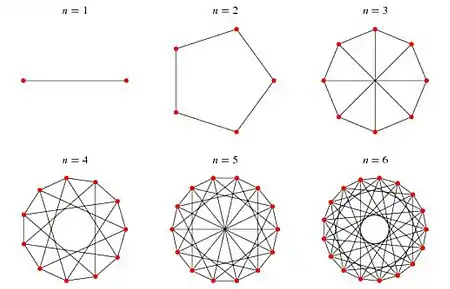 |
Propriétés
Les graphes d'Andrásfai sont sans triangle, et le graphe And(n) a un nombre d'indépendance (taille maximale d'un ensemble stable) égal à . Il en résulte la formule , où est le nombre de Ramsey. L'égalité vaut seulement pour .
Les graphes d'Andrásfai ont la propriété que tout ensemble stable (i. e. de sommets non connectés) maximal est formé des voisins d'un sommet commun. Par exemple, dans le graphe And(3), les trois voisins d'un sommet, à savoir ses voisins sur le cercle et celui qui lui est opposé, forment un ensemble stable maximal[2].
Notes et références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Andrásfai graph » (voir la liste des auteurs).
Bibliographie
- Chris Godsil et Gordon F. Royle, Algebraic Graph Theory, Springer, coll. « Graduate Texts in Mathematics » (no 207), (1re éd. 2001) (ISBN 978-1-4613-0163-9), « §6.10–6.12: The Andrásfai Graphs—Andrásfai Coloring Graphs, A Characterization », p. 118–123.
- (hu) Béla Andrásfai, Ismerkedés a gráfelmélettel, Budapest, Tankönyvkiadó, , 132–5 p. (OCLC 908973331).
- Béla Andrásfai, « Graphentheoretische Extremalprobleme », Acta Math. Acad. Sci. Hungar., vol. 15, , p. 413-438
- Béla Andrásfai, Introductory Graph Theory, Elmsford, NY, Pergamon Press,
- Andries E. Brouwer, « Finite Graphs in Which the Point Neighbourhoods Are the Maximal Independent Sets », dans From Universal Morphisms to Megabytes: A Baayen Space Odyssey, Amsterdam, Math. Centrum Wisk. Inform., , p. 231-233
- János Pach, « Graphs Whose Every Independent Set Has a Common Neighbour », Discrete Math., vol. 31, , p. 217-228 (DOI 10.1016/0012-365X(81)90221-1, lire en ligne)
- Tomasz Łuczak, Joanna Polcyn et Christian Reiher, « Andrásfai and Vega graphs in Ramsey-Turán theory », submitted, (arXiv 2002.01498)
- Tomasz Łuczak, Joanna Polcyn et Christian Reiher, « On the Ramsey-Turán density of triangles », submitted, (arXiv 2001.11474)
- Wiebke Bedenknecht, Guilherme Oliveira Mota, Christian Reiher et Mathias Schacht, « On the local density problem for graphs of given odd-girth », Electronic Notes in Discrete Mathematics, vol. 62, , p. 39–44 (DOI 10.1016/j.endm.2017.10.008, arXiv 1609.05712).
Articles connexes
Lien externe
- (en) Eric W. Weisstein, « Andrásfai Graph », sur MathWorld








