Graphe conceptuel
Un graphe conceptuel est un formalisme de représentation de connaissances et de raisonnements. Ce formalisme a été introduit par John F. Sowa (en) en 1984. Depuis cette date, ce formalisme a été développé suivant trois directions principales : interface graphique de la logique du premier ordre, système diagrammatique pour la logique du premier ordre, formalisme de représentation de connaissances et de raisonnement basé sur les graphes.
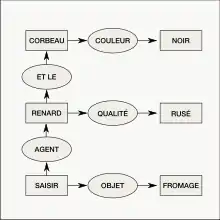
Une interface graphique de la logique du premier ordre
Dans cette approche les graphes conceptuels servent d'interface graphique pour la logique du premier ordre (calcul des prédicats). Une formule logique est représentée par un graphe biparti étiqueté, les sommets d'une des deux classes représentant les prédicats et les sommets de l'autre classe représentant les arguments de ces prédicats. À ce titre, les graphes conceptuels constituent l'un des formats proposés par l'ISO dans le cadre de la Common Logic. Dans cette approche le modèle n'a pas de mécanismes spécifiques de raisonnement. Pour faire des raisonnements les graphes sont traduits par des formules de logique, puis un démonstrateur logique doit être utilisé.
Un système diagrammatique pour la logique du premier ordre
Une autre direction poursuit dans la voie des graphes existentiels de Charles Sanders Peirce, qui étaient une des origines des graphes conceptuels tels que proposés par Sowa. Dans cette approche, développée, en particulier, par Dau, plutôt que des graphes au sens de la théorie des graphes, les graphes conceptuels sont des diagrammes, et les opérations de raisonnement sont effectuées par des opérations sur ces diagrammes. Ces opérations sur les diagrammes sont difficilement automatisables.
Un formalisme de représentation de connaissances et de raisonnement basé sur les graphes
Les graphes, au sens classique de la théorie des graphes, sont au cœur du troisième point de vue développé, en particulier, par Chein et Mugnier et le groupe de Montpellier. Les connaissances sont, comme dans les deux approches précédentes, représentées par des graphes étiquetés mais cette fois-ci les mécanismes de raisonnement sont basés sur des opérations de graphes, en particulier sur l'homomorphisme de graphes (cette opération était appelée 'projection' dans les premiers travaux sur les graphes conceptuels, mais cette opération est sans relation avec l'opération appelée projection dans les bases de données). Cette troisième approche n'est pas indépendante de la logique puisque les graphes conceptuels peuvent être munis d'une sémantique en logique du premier ordre et que les raisonnements basés sur l'homomorphisme de graphes sont corrects et complets pour cette sémantique. Dit simplement, toutes les inférences faites en logique peuvent être faites par des opérations de graphes et réciproquement. L'un des intérêts essentiels de cette approche est de pouvoir utiliser des algorithmes de graphes qui s'avèrent efficaces pour faire des raisonnements. Le problème de base, l'interrogation par une requête qui est un graphe conceptuel, d'une base de graphes conceptuels, est un problème NP-complet mais qui est polynomial en la taille de la base de graphes (cf. la « data complexity » utilisée en bases de données). Cette approche permet également de voir les liens entre les graphes conceptuels et les bases de données ou la satisfaction de contraintes.
Graphes conceptuels et logique de description
L'approche « graphes » des graphes conceptuels peut être comparée aux logiques de description. En effet, ces deux modèles peuvent être considérés comme issus des réseaux sémantiques. En séparant la représentation de connaissances ontologiques et de connaissances factuelles, et en étant munis d'une sémantique logique, ils répondent, tous les deux, aux critiques essentielles faites aux réseaux sémantiques. De plus, ils s'attachent tous les deux, à trouver des compromis entre pouvoir expressif et complexité des raisonnements.
Bibliographie
- Chein M., Mugnier M.-L., Graph-based Knowledge Representation: Computational Foundations of Conceptual Graphs, Springer, 2009. (ISBN 978-1-84800-286-9)()
- Dau, F., The Logic System of Concept Graphs with Negation and Its Relationship to Predicate Logic, volume 2892 of LNCS, Springer, 2003.
- Sowa, J.F., « Conceptual Graphs for a Data Base Interface », IBM Journal of Research and Development 20(4), 336–357, 1976.(Fichier PDF)
- Sowa J. F., Conceptual Structures : Information Processing in Mind and Machine, Addison-Wesley, (ISBN 0-201-14472-7), 1984