Force d'un graphe
En théorie des graphes, la force d'un graphe (strength en anglais) non orienté est le plus petit rapport entre le nombre d'arêtes supprimées et le nombre de composantes créées dans une décomposition du graphe.
| Force d'un graphe (exemple) | |
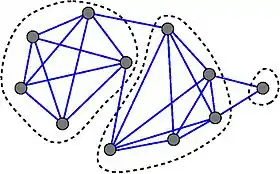 Un graphe de force 2 : le graphe est décomposé en trois parties avec un total de 4 arêtes entre les composantes, ce qui donne le rapport 4/(3-1)=2. | |
Définition
Soit un graphe non orienté. Soit l'ensemble des partitions de , et, pour toute partition , soit l'ensemble des arêtes qui relient des parties de la partition . La force est :
- .
Pour une partition des sommets, est l'ensemble de toutes les arêtes reliant des parties de la partition. Pour qu'il y ait une arête au moins entre deux des composantes, on doit choisir arêtes de façon appropriée ; la force est le plus petit rapport des deux entiers.
Par formulation en programmation linéaire, on a des définitions équivalentes : Soit l'ensemble des arbres couvrant de G. Alors
- avec les contraintes : et .
ou, par dualité en programmation linéaire :
- avec les contraintes : et .
Complexité du calcul
Le calcul de la force d'un graphe peut être fait en temps polynomial ; le premier algorithme de ce type a été décrit par Cunningham[1] en 1985. L'algorithme avec la meilleure complexité est dû à Trubin (1993) ; en utilisant la décomposition des flots de Goldberg et Rao (1998)[2], il est en complexité en temps pour un graphe à n sommets et m arêtes.
Propriétés
- Soit un graphe non orienté et soit un entier positif. La taille maximale d'une union de forêts est égale à la plus petite valeur de
- prise sur toutes les partitions de [3].
- Si est une partition qui maximise , et si est la restriction de G à l'ensemble , alors .
- Théorème de Tutte-Nash-Williams. — Un graphe contient k arbres couvrants à arêtes disjointes si et seulement si
- pour toute partition de .[4]
- Le théorème de Tutte-Nash-Williams s'exprime avec la notion de force : est le nombre maximum d'arbres couvrant à arêtes disjointes qui peuvent être contenus dans G.
- Contrairement au problème de partitionnement d'un graphe, les partitions produites par le calcul de la force ne sont pas nécessairement équilibrées (c'est-à-dire ne sont pas de taille presque égale).
Notes et références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Strength of a graph » (voir la liste des auteurs).
- (en) William H. Cunningham, « Optimal attack and reinforcement of a network », Journal of the ACM, vol. 32, no 3, , p. 549–561 (ISSN 0004-5411 et 1557-735X, DOI 10.1145/3828.3829, lire en ligne, consulté le )
- Goldberg et Rao 1998.
- Shrijver 2003, (Theorem 51.1).
- Shrijver 2003, (Corollary 51.1a).
Bibliographie
- Alexander Schrijver, Combinatorial Optimization, Springer, (ISBN 978-3-540-44389-6), Chapitre 51.
- William H. Cunningham, « Optimal attack and reinforcement of a network », Journal of the ACM, vol. 32, no 3, , p. 549–561 (DOI 10.1145/3828.3829)
- V. A. Trubin, « Strength of a graph and packing of trees and branchings », Cybernetics and Systems Analysis, vol. 29, no 3, , p. 379–384 (DOI 10.1007/BF01125543)
- Andrew V. Goldberg et Satish Rao, « Beyond the flow decomposition barrier », Journal of the ACM, vol. 45, no 5, , p. 783-797 (DOI 10.1145/290179.290181)
Articles connexes
- Dureté d'un graphe, un concept analogue pour les suppressions de sommets
- Théorème de Nash-Williams (en)
- Lexique de la théorie des graphes

























