Fonction omega de Wright
En mathématiques, la fonction omega de Wright ou fonction de Wright[note 1] dénotée ω, est définie à partir de la fonction W de Lambert par :

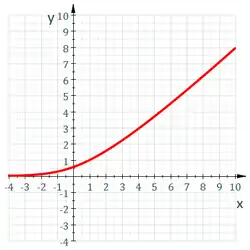
La fonction omega de Wright le long de l'axe réel.
Utilisation
Une des principales applications de cette fonction est dans la résolution de l'équation z = ln(z), comme l'unique solution est donnée par z = e−i π ω.
La valeur y = ω(z) est l'unique solution, quand  pour x ≤ −1, de l'équation y + ln(y) = z. A l'exception de ces deux rayons, la fonction omega de Wright est continue, et même analytique.
pour x ≤ −1, de l'équation y + ln(y) = z. A l'exception de ces deux rayons, la fonction omega de Wright est continue, et même analytique.
Propriétés
La fonction omega de Wright satisfait la relation Wk(z) = ω(ln(z) + 2 π i k).
Elle vérifie aussi l'équation différentielle

partout où ω est analytique (ce qui peut se voir avec une séparation de variables et en utilisant l'équation ω + ln(ω) = z), et par conséquent sa primitive peut s'écrire :

Sa série de Taylor autour du point ωa + ln(ωa) = a prend la forme :

avec

avec

désignant les nombres eulériens seconde espèce.
Valeurs spéciales

Tracés
- Tracés de la fonction omega de Wright sur le plan complexe
z = Re(ω(x + i y))
z = Im(ω(x + i y))
ω(x + i y)
Notes
- À ne pas confondre avec la fonction de Fox-Wright (en), aussi parfois appelée fonction de Wright.
Références
Cet article est issu de
wikipedia. Text licence:
CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.

 z = Re(ω(x + i y))
z = Re(ω(x + i y)) z = Im(ω(x + i y))
z = Im(ω(x + i y)) ω(x + i y)
ω(x + i y)






