Fenêtrage

Pour observer un signal sur une durée finie, on le multiplie par une fonction fenêtre d'observation (également appelée fenêtre de pondération ou d'apodisation[1]). La plus simple est la fenêtre rectangulaire (ou porte), définie telle que :

${\displaystyle h(t)={\begin{cases}1&{\mbox{ si }}t\in [T_{1},T_{2}]\\0&{\mbox{ sinon.}}\end{cases}}}$

Ainsi, quand on multiplie un signal s(t) par cette fenêtre, on n'obtient plus que la partie comprise entre T₁ et T₂ de ce signal : on l'« observe » sur une durée allant de T₁ à T₂. Toute observation étant de durée limitée, on applique forcément une fenêtre par rapport à un signal théorique infini ; on utilise donc au moins une fenêtre, même si on l'applique sans s'en rendre compte.

Au lieu d'étudier le signal s(t), on étudie le signal tronqué : s_h(t) = s(t)h(t) ; en passant dans le domaine fréquentiel via une transformée de Fourier (TF), on obtient[2] - [3] le produit de convolution S_h(h) = (S ∗ H)(f), où H(f) est la TF de la fenêtre.

L'utilisation d'une fenêtre de pondération va donc changer la transformée de Fourier du signal.

Allures temporelles de quelques fenêtres.

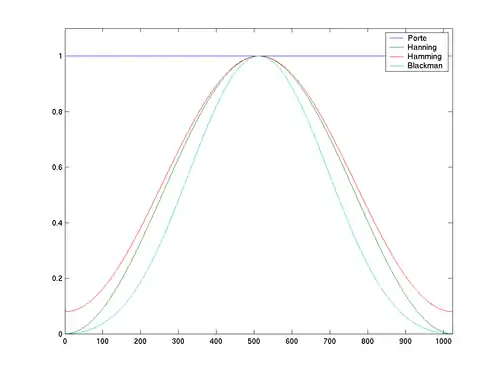
Fenêtre rectangulaire, qui conduit à l'approximation sigma : ${\displaystyle h(t)={\begin{cases}1&{\mbox{ si }}t\in [0,T]\\0&{\mbox{ sinon.}}\end{cases}}}$

Fenêtre triangulaire (de Bartlett) : ${\displaystyle h(t)={\begin{cases}{\frac {2t}{T}}&{\mbox{ si }}t\in [0,{\frac {T}{2}}[\\{\frac {2(T-t)}{T}}&{\mbox{ si }}t\in [{\frac {T}{2}},T]\\0&{\mbox{ sinon.}}\end{cases}}}$

Fenêtre de Hann : ${\displaystyle h(t)={\begin{cases}{\frac {1}{2}}-{\frac {1}{2}}\cos(2\pi {\frac {t}{T}})&{\mbox{ si }}t\in [0,T]\\0&{\mbox{ sinon.}}\end{cases}}}$

Fenêtre de Hamming[2] : ${\displaystyle h(t)={\begin{cases}0,54-0,46\cos(2\pi {\frac {t}{T}})&{\mbox{ si }}t\in [0,T]\\0&{\mbox{ sinon.}}\end{cases}}}$

Fenêtre de Blackman : ${\displaystyle h(t)={\begin{cases}0,42-0,5\cos(2\pi {\frac {t}{T}})+0,08\cos(4\pi {\frac {t}{T}})&{\mbox{ si }}t\in [0,T]\\0&{\mbox{ sinon.}}\end{cases}}}$

Et d'autres : fenêtres de Kaiser (en) (de paramètre ${\displaystyle \alpha }$), gaussienne, flat top, en cosinus relevé…

À noter : la fenêtre de Hann est quelquefois appelée « fenêtre de Hanning », peut-être par analogie avec la « fenêtre de Hamming ». C'est incorrect, ces noms sont en fait issus des noms de leurs inventeurs (respectivement Julius von Hann et Richard Hamming).

La TF du signal analysé est convoluée avec la TF de la fenêtre ; dans l'idéal, pour ne pas biaiser le spectre initial, il faudra que l'allure de la fenêtre spectrale soit une fonction de Dirac. Or, le signal temporel ayant un spectre en fonction de dirac est un signal constant infini, ce qui est impossible en pratique.

Les allures spectrales des fenêtres de pondérations présentent une succession de lobes : pour se rapprocher d'une fonction de Dirac, il faut que le lobe principal soit le plus étroit possible, tandis que les lobes secondaires doivent être les plus faibles possible. Plus le lobe principal d'une fenêtre aura tendance à être étroit, plus ses lobes secondaires seront importants...

Il y a donc toujours un compromis à faire entre largeur du lobe principal et importance des lobes secondaires.

Quelques visualisations dans le domaine des fréquences, les représentations sont linéaires à gauche, logarithmiques à droite (cliquez pour agrandir) :

Allures fréquentielles de quelques fenêtres

Allures fréquentielles de quelques fenêtres

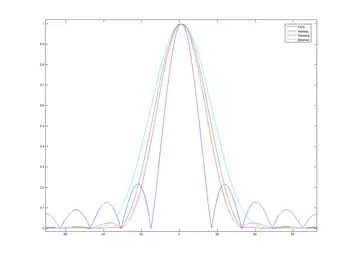
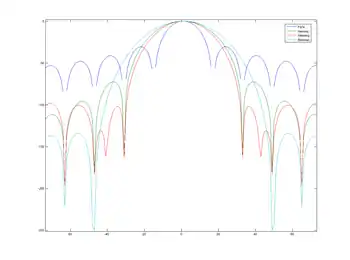
On remarque que la fenêtre rectangulaire a le lobe principal le plus étroit, mais ses lobes secondaires sont les plus importants ; au contraire, celle de Blackman a les plus faibles lobes secondaires, mais un lobe principal plus large. Le type de fenêtre est à choisir selon ce qu'on souhaite observer d'un spectre : la localisation des maximums, la localisation de l'énergie selon les fréquences, la valeur des maximums, etc.

Voici les principales caractéristiques des fenêtres d'analyse courantes :

Plus la fenêtre choisie aura une grande durée temporelle, plus elle sera étroite dans le domaine fréquentiel. Ainsi, en prenant une fenêtre infiniment longue temporellement, on aboutit à la limite à un dirac en fréquence, qui est l'élément neutre du produit de convolution.

Ainsi, pour une fenêtre infiniment longue, on retrouve le spectre « réel » du signal analysé, qui correspond effectivement à la TFD d'un signal de durée infinie.