Approximation sigma

Comparaison animée de l'approximation d'un signal carré (en rouge) par sa série de Fourier (en bleu) et par son approximation sigma (en vert). On voit le phénomène de Gibbs apparaître au niveau des discontinuités alors que l'approximation sigma approche le carré de façon plus lisse.

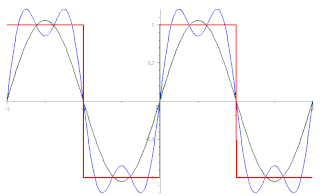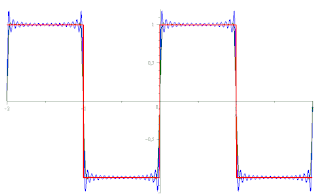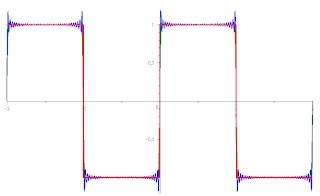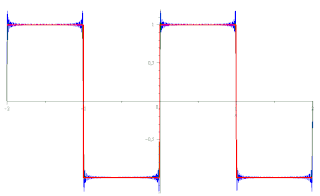
Une approximation sigma appliquée à une série de période T peut s'écrire :

${\displaystyle s(\theta )={\frac {1}{2}}a_{0}+\sum _{k=1}^{m-1}\mathrm {sinc} \left({\frac {k}{m}}\right)\cdot \left[a_{k}\cos \left({\frac {2\pi k}{T}}\theta \right)+b_{k}\sin \left({\frac {2\pi k}{T}}\theta \right)\right],}$

selon la fonction sinus cardinal normalisée

${\displaystyle \mathrm {sinc} (x)={\frac {\sin(\pi x)}{\pi x}}.}$

où le terme

${\displaystyle \mathrm {sinc} {\Bigl (}{\frac {k}{m}}{\Bigr )}}$

est le « facteur σ de Lanczos » qui est à l'origine de la suppression de la plus grande partie des oscillations supplémentaires dues au phénomène de Gibbs par atténuation des grandes valeurs des coefficients de Fourier associés. Il ne résout cependant pas tout à fait le problème, mais dans les cas extrêmes on peut mettre l'expression au carré, ou même au cube, ou plus simplement recourir aux sommes de Fejér.

L'idée de Lanczos consiste à atténuer les coefficients de Fourier d’ordre élevé, qui rendent la série localement divergente. Il étudie ainsi les cas où la dérivée de la série de Fourier peut fortement varier localement. En effet, pour une somme partielle d'une fonction développée en série de Fourier de la forme

${\displaystyle f_{m}(x)=\sum _{k=-(m-1)}^{m-1}c_{k}{\rm {e}}^{\mathrm {i} kx},}$

on pose

${\displaystyle \rho _{m}(x)=\sum _{k=0}^{+\infty }c_{m+k}{\rm {e}}^{\mathrm {i} kx}.}$

Le reste de la série de Fourier s'exprime alors sous la forme

${\displaystyle R_{m}(x)=f(x)-f_{m}(x)={\rm {e}}^{\mathrm {i} mx}\rho _{m}(x)+{\rm {e}}^{-\mathrm {i} mx}\rho _{-m}(x).}$

Lanczos remarque que dans le cas général, ρ_m(x) a la forme d'une onde porteuse lisse modulée de haute fréquence, donc la dérivée du reste

${\displaystyle R_{m}'(x)=\mathrm {i} m({\rm {e}}^{\mathrm {i} mx}\rho _{m}(x)-{\rm {e}}^{-\mathrm {i} mx}\rho _{-m}(x))+{\rm {e}}^{\mathrm {i} mx}\rho _{m}'(x)+{\rm {e}}^{-\mathrm {i} mx}\rho _{-m}'(x),}$

va prendre de grandes valeurs si le reste ne converge pas « assez vite ». Il pose ainsi un opérateur de différentiation adapté :

${\displaystyle \mathrm {D} _{m}f(x)={\frac {f\left(x+{\frac {\pi }{m}}\right)-f\left(x-{\frac {\pi }{m}}\right)}{\frac {2\pi }{m}}},}$

qui tend bien vers l'opérateur de dérivation pour m grand, mais donne

${\displaystyle \mathrm {D} _{m}R_{m}(x)=-{\rm {e}}^{\mathrm {i} mx}\mathrm {D} _{m}\rho _{m}(x)-{\rm {e}}^{-\mathrm {i} mx}\mathrm {D} _{m}\rho _{-m}(x),}$

et les fonctions ρ_m(x), ρ_–m(x) sont suffisamment lisses pour que les valeurs de leurs dérivées n'aient pas d'impact majeur sur l'erreur. En remarquant que

${\displaystyle \mathrm {D} _{m}({\rm {e}}^{\mathrm {i} kx})={\frac {\sin({\frac {\pi k}{m}})}{\frac {\pi }{m}}}\times \mathrm {i} k{\rm {e}}^{\mathrm {i} kx},}$

on voit qu'utiliser cet opérateur de différentiation revient à multiplier les coefficients de Fourier par un facteur σ.

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Sigma approximation » (voir la liste des auteurs).
• (en) Cornelius Lanczos, Linear Differential Operators, Londres & New York, éd. van Nostrand, 1961 (réimpr. 1997) (ISBN 0-486-68035-5), « Local smoothing by integration »
• (en) Cornelius Lanczos, Applied Analysis, New York, Prentice-Hall, 1956, 539 p. (ISBN 978-0-486-65656-4, BNF 37364956)
• (en) Forman S. Acton, Numerical Methods That (Usually) Work, Washington(D.C.), The Mathematical Association of America, 1970 (réimpr. 1997), 549 p. (ISBN 978-0-88385-450-1, BNF 37366302), « Fourier Series »