Facteur de forme (rayonnement thermique)
En physique, le facteur de forme est la part du rayonnement thermique, émis par une surface, qu'une autre surface reçoit. Il est plus précisément la fraction du flux thermique rayonné par une surface isotherme et à émission isotrope (« lambertienne ») reçue par une autre surface dans un milieu non participatif (pas d'émission, d'absorption ou de diffusion en volume). Cette quantité ne dépend que de la géométrie du milieu.
Ce type de problème se rencontre dans les transferts thermiques[1] - [2] ou le rendu en génération d'images de synthèse[3].
Quantités caractérisant le rayonnement
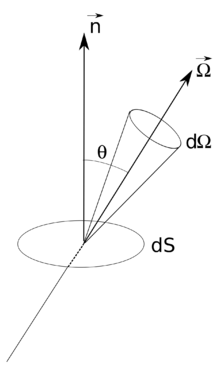
Pour caractériser le transfert de rayonnement on utilise :
- la luminance spectrale (par unité de fréquence, en J m−2 sr−1) définie comme la quantité d'énergie radiative contenue dans un intervalle spectral , dans un angle solide , traversant l'aire élémentaire durant le temps
On peut également utiliser les quantités correspondantes rapportées à la longueur d'onde au lieu de la fréquence.
Définition du facteur de forme
Aspect local

Deux surfaces élémentaires et distantes de échangent du rayonnement. Le flux spectral reçu par est
où est l'angle solide sous lequel on voit depuis .
Par suite on peut écrire
avec
Cette quantité caractérise entièrement la géométrie de manière immédiatement utilisable pour le calcul des échanges radiatifs.
On a par symétrie . Par convention (l'interprétation physique est évidente).
Aspect intégral
Soient des surfaces quelconques.
Le flux spectral reçu de la surface par la surface s'écrit
Si l'émission est isotrope la loi de Lambert permet d'écrire le flux spectral sous la forme . Si de plus on considère cette quantité constante sur la surface on a
où
est appelé facteur de forme (en anglais view factor). Il représente la fraction de l'énergie émise par arrivant sur .
Du fait des hypothèses faites, cette notion n'est valide que dans un domaine limité. Elle a dans ce domaine l'avantage de permettre des calculs analytiques sur un grand nombre de configurations géométriques simples[2] - [4].
Propriétés
- dans le cas de géométries planes ou convexes mais pour une partie concave.
- Puisque on déduit de l'expression ci-dessus un principe de réciprocité
- De la définition on déduit très facilement une relation d'additivité utilisable pour les géométries simples[2]
Une formulation équivalente
Quel que soit le mode de description d'une surface, celle-ci dépend de deux variables. L'expression du facteur de forme ci-dessus est donc une intégrale quadruple. On peut réduire cette dimension en utilisant le théorème de Stokes. Soient les contours de , les éléments de ces lignes et la distance entre ces éléments, alors le facteur de forme s'écrit comme une intégrale de bord[2]
On a réduit l'expression à une intégrale double dont le calcul est plus simple.
Calcul numérique des facteurs de forme
L'étape importante lorsque l'on utilise la première expression du facteur de forme est le calcul de l'angle solide . La méthode de lancer de rayon est utilisable et résout simplement le problème des parties cachées. Pour le calcul des facteurs de forme proprement dit le calcul analytique est préférable. Lorsque la vitesse de calcul est importante, par exemple pour la génération d'images, on peut utiliser une méthode approchée utilisant des hémicubes.
Code de calcul en libre accès
Notes et références
- (en) Michael M. Modest, Radiative Heat Transfer, Academic Press, 2003 (ISBN 0-12-503163-7).
- (en) John R. Howell, M. Pinar Menguç, Robert Siegel, Thermal Radiation Heat Transfer, CRC Press, 2010 (ISBN 1-43-980533-4).
- (en) Jeffrey J. McConnell, Anthony Ralston, Edwin D. Reilly, David Hemmendinger, Computer Graphics Companion, Wiley, 2002 (ISBN 978-0-470-86516-3).
- (en) John R. Howell, « A Catalog of Radiation Heat Transfer Configuration Factors ».


































