Effet Pearson-Anson

lampe au néon NE-2

Une ampoule au néon, souvent utilisée comme lampe témoin dans les appareils, est constituée d'une ampoule en verre contenant deux électrodes, séparées par un gaz inerte tel que le néon à basse pression. Ses caractéristiques courant-tension non linéaires (schéma ci-dessous) lui permettent de fonctionner comme un dispositif de commutation[13].

Lorsqu'une tension est appliquée aux électrodes, le gaz ne conduit pratiquement aucun courant électrique jusqu'à ce qu'une tension seuil soit atteinte (point b), appelée tension d'amorçage ou de claquage, V_b[7] - [14]. À cette tension, les électrons du gaz sont accélérés à une vitesse suffisante pour arracher d'autres électrons aux atomes du gaz, lesquels arrachent à leur tour d'autres électrons dans une réaction en chaîne. Le gaz contenu dans l'ampoule s'ionise, provoquant une décharge lumineuse, et sa résistance chute à une faible valeur. Dans son état conducteur, le courant traversant l'ampoule n'est limité que par le circuit externe. La tension aux bornes de l'ampoule chute à une tension inférieure appelée tension de maintien V_m. L'ampoule continuera à conduire le courant jusqu'à ce que la tension appliquée tombe en dessous de la tension d'extinction V_e (point d), qui est généralement proche de la tension de maintien. En dessous de cette tension, le courant ne fournit pas assez d'énergie pour maintenir l'ionisation du gaz, et l'ampoule revient à son état non conducteur à haute résistance (point a).

La tension d'allumage V_b de l'ampoule est supérieure à sa tension d'extinction V_e. Cette propriété, appelée hystérésis, permet à l'ampoule de fonctionner comme un oscillateur. L'hystérésis est due à la résistance négative de l'ampoule, à la chute de la tension lorsque le courant augmente après le claquage[7] - [14], qui est une propriété de toutes les lampes à décharge.

Jusqu'aux années 1960, les oscillateurs à dents de scie étaient également construits avec des thyratrons[15] - [16]. Il s'agissait de tubes électroniques triodes remplis de gaz. Ils fonctionnaient un peu comme les ampoules au néon, le tube ne conduisant pas jusqu'à ce que la tension cathode-anode atteigne une tension de claquage. L'avantage du thyratron était que la tension de claquage pouvait être contrôlée par la tension de la grille[16]. Cela permettait de modifier électroniquement la fréquence de l'oscillation. Les oscillateurs Thyratron étaient utilisés comme bases de temps dans les oscilloscopes[16].

Courbe IV d'une ampoule au néon (droite)[7] montrant la boucle d'hystérésis de l'oscillateur (abcd), la ligne de charge (bleu) et les formes d'onde de sortie (à gauche). La ligne de charge doit se trouver dans la zone ombrée pour que le circuit oscille. v est la tension aux bornes de l'ampoule au néon et i est le courant qui la traverse.

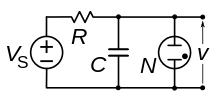
Dans le circuit de l'oscillateur Pearson-Anson (en haut), un condensateur C est connecté à l'ampoule au néon N[7]. Le condensateur est continuellement chargé par le courant traversant la résistance R jusqu'à ce que l'ampoule conduise, le déchargeant à nouveau, après quoi il se charge à nouveau[17]. Le cycle détaillé est illustré par la boucle d'hystérésis abcd sur le diagramme courant-tension à droite[4] - [7] - [10] :

• Lorsque la tension d'alimentation est activée, l'ampoule au néon est dans sa condition de haute résistance et se comporte comme un circuit ouvert. Le courant qui traverse la résistance commence à charger le condensateur et sa tension commence à augmenter vers la tension d'alimentation.
• Lorsque la tension aux bornes du condensateur atteint b, la tension de claquage de l'ampoule V_b, l'ampoule s'allume et sa résistance chute à une faible valeur. La charge du condensateur se décharge rapidement dans l'ampoule par une impulsion de courant momentanée (c). Lorsque la tension tombe à la tension d'extinction V_e de l'ampoule (d), l'ampoule s'éteint et le courant qui la traverse tombe à un faible niveau (a). Le courant qui traverse la résistance recommence à charger le condensateur, et le cycle se répète.

Le circuit fonctionne donc comme un oscillateur de relaxation à basse fréquence, la tension du condensateur oscillant entre les tensions de claquage et d'extinction de l'ampoule en une onde en dents de scie. La période est proportionnelle à la constante de temps RC.

La lampe au néon produit un bref flash lumineux à chaque fois qu'elle se met en marche, de sorte que le circuit peut également être utilisé comme un circuit "clignotant". La double fonction de la lampe, à la fois source de lumière et dispositif de commutation, permet au circuit de compter moins de pièces et de coûter moins cher que de nombreux autres circuits de clignotants.

La tension d'alimentation V_s doit être supérieure à la tension de claquage de l'ampoule V_b, sinon l'ampoule ne pourra jamais conduire[7]. La plupart des petites lampes au néon ont des tensions de claquage comprises entre 80 et 150 volts. Si la tension d'alimentation est proche de la tension de claquage, la tension du condensateur sera dans la "queue" de sa courbe exponentielle au moment où elle atteindra V_b, de sorte que la fréquence dépendra de manière sensible du seuil de claquage et des niveaux de tension d'alimentation, entraînant des variations de fréquence[17]. Par conséquent, la tension d'alimentation est généralement nettement supérieure à la tension d'allumage de l'ampoule[7]. Cela rend également la charge plus linéaire et l'onde en dents de scie plus triangulaire[17].

La résistance R doit également être comprise dans une certaine plage de valeurs pour que le circuit oscille[7]. Ceci est illustré par la ligne de charge (bleue) sur le graphique IV. La pente de la ligne de charge est égale à R. Les points de fonctionnement possibles du circuit en courant continu se trouvent à l'intersection de la ligne de charge et de la courbe IV de la lampe au néon (noir). Pour que le circuit soit instable et oscille, la ligne de charge doit couper la courbe IV dans sa région de résistance négative, entre b et d, où la tension diminue avec l'augmentation du courant[7].

Ce point est défini par la région ombrée sur le diagramme. Si la ligne de charge croise la courbe IV à l'endroit où elle présente une résistance positive, en dehors de la zone ombrée, cela représente un point de fonctionnement stable, de sorte que le circuit n'oscille pas :

• Si R est trop grand, du même ordre que la résistance de fuite de l'ampoule à l'état "éteint", la ligne de charge croisera la courbe IV entre l'origine et b. Dans cette région, le courant traversant R depuis l'alimentation est si faible que le courant de fuite à travers l'ampoule l'absorbe, de sorte que la tension du condensateur n'atteint jamais V_b et que l'ampoule ne s'allume jamais[7]. La résistance de fuite de la plupart des ampoules néon est supérieure à 100MΩ, ce n'est donc pas une limitation sérieuse.
• Si R est trop petit, la ligne de charge croisera la courbe IV entre c et d. Dans cette région, le courant à travers R est trop important ; une fois l'ampoule allumée, le courant à travers R sera suffisamment important pour qu'il reste conducteur sans le courant du condensateur, et la tension aux bornes de l'ampoule ne tombera jamais à V_e, de sorte que l'ampoule ne s'éteindra jamais[7].

Les petites ampoules au néon oscillent généralement avec des valeurs de R comprises entre 500kΩ et 20MΩ[7]. Si C n'est pas petit, il peut être nécessaire d'ajouter une résistance en série avec l'ampoule au néon, pour limiter le courant qui la traverse afin d'éviter tout dommage lorsque le condensateur se décharge[10]. Cela augmentera le temps de décharge et diminuera légèrement la fréquence, mais son effet sera négligeable aux basses fréquences.

La période d'oscillation peut être calculée à partir des seuils de tension de claquage et d'extinction de la lampe utilisée[6] - [7] - [10] - [18]. Pendant la période de charge, l'ampoule présente une résistance élevée et peut être considérée comme un circuit ouvert, de sorte que le reste de l'oscillateur constitue un circuit RC, la tension du condensateur approchant V_s de manière exponentielle, avec une constante de temps RC. Si v(t) est la tension de sortie aux bornes du condensateur.

Derivation dev(t)

Derivation de v(t) et i(t) est le courant à travers la résistance

${\displaystyle V_{S}=v+Ri\,}$ et ${\displaystyle i=C{dv \over dt}\,}$

donc l'équation différentielle du circuit est

${\displaystyle RC{dv \over dt}+v=V_{S}\,}$

La solution géneral est

${\displaystyle v(t)=A_{1}e^{-t/RC}+A_{2}\,}$

Application des conditions limites ${\displaystyle v(\infty )=A_{2}=V_{S}\,}$ et ${\displaystyle v(0)=A_{1}+V_{S}=0\,}$donne les constantes A1 et A2, donc la solution est

${\displaystyle v(t)=V_{S}(1-e^{-t/RC})\,}$

La solution pour le temps

${\displaystyle t=RC\ln {\Bigl [}{V_{S} \over {V_{S}-v}}{\Bigr ]}\,}$

Bien que la première période soit plus longue que les autres parce que la tension part de zéro, les formes d'onde de tension des périodes suivantes sont identiques à la première entre Ve et V_b. La période T est donc l'intervalle entre le moment où la tension atteint V_e et le moment où la tension atteint V_b.

${\displaystyle T=t(V_{b})-t(V_{e})\,}$

${\displaystyle T=RC\ln {\Bigl [}{V_{S} \over {V_{S}-V_{b}}}{\Bigr ]}-RC\ln {\Bigl [}{V_{S} \over {V_{S}-V_{e}}}{\Bigr ]}\,}$

${\displaystyle T=RC\ln {\Bigl [}{{V_{S}-V_{e}} \over {V_{S}-V_{b}}}{\Bigr ]}\,}$

Cette formule n'est valable que pour des fréquences d'oscillation allant jusqu'à 200 Hz environ[7], au-dessus de cette valeur, divers délais font que la fréquence réelle est inférieure à cette valeur[8]. En raison du temps nécessaire pour ioniser et déioniser le gaz, les lampes au néon sont des dispositifs à commutation lente, et l'oscillateur de la lampe au néon est limité à une fréquence maximale d'environ 20 kHz[7] - [8] - [10]. Les tensions de claquage et d'extinction des lampes au néon peuvent varier entre des pièces similaires[17], les fabricants ne spécifient généralement que de larges plages pour ces paramètres. Ainsi, si une fréquence précise est souhaitée, le circuit doit être ajusté par essais et erreurs[17]. Les seuils changent également avec la température, de sorte que la fréquence des oscillateurs à lampe au néon n'est pas particulièrement stable[10].

Comme d'autres oscillateurs à relaxation, l'oscillateur à ampoule au néon a une faible stabilité de fréquence, mais il peut être synchronisé (entraîné) par une tension périodique externe appliquée en série avec l'ampoule au néon. Même si la fréquence externe est différente de la fréquence naturelle de l'oscillateur, les pics du signal appliqué peuvent dépasser le seuil de claquage de l'ampoule, déchargeant le condensateur prématurément, de sorte que la période de l'oscillateur est verrouillée sur le signal appliqué[19].

Un comportement intéressant peut résulter de la variation de l'amplitude et de la fréquence de la tension externe. Par exemple, l'oscillateur peut produire une tension oscillante dont la fréquence est un sous-multiple de la fréquence externe. Ce phénomène, connu sous le nom de "sous-multiplication" ou "démultiplication", a été observé pour la première fois en 1927 par Balthasar van der Pol et son collaborateur Jan van der Mark[20] - [21]. Dans certains cas, le rapport entre la fréquence externe et la fréquence de l'oscillation observée dans le circuit peut être un nombre rationnel, voire irrationnel (ce dernier cas est connu comme le régime "quasi-périodique")[19]. Lorsque les régimes périodique et quasi-périodique se chevauchent, le comportement du circuit peut devenir apériodique, ce qui signifie que le motif des oscillations ne se répète jamais. Cette apériodicité correspond à un comportement chaotique du circuit[19] - [21].

L'oscillateur forcé à ampoule de néon a été le premier système dans lequel un comportement chaotique a été observé[22]. Van der Pol et van der Mark ont écrit, à propos de leurs expériences de démultiplication, que : "Souvent, un bruit irrégulier est entendu dans les récepteurs téléphoniques avant que la fréquence ne saute à la valeur inférieure suivante. Il s'agit toutefois d'un phénomène subsidiaire, l'effet principal étant la démultiplication régulière de la fréquence"[20].

Toute oscillation périodique aurait produit un son musical ; seules les oscillations apériodiques, chaotiques, produiraient un "bruit irrégulier". On pense qu'il s'agit de la première observation du chaos, bien que van der Pol et van der Mark n'aient pas réalisé son importance à l'époque[19] - [21] - [22].

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Pearson–Anson effect » (voir la liste des auteurs).

• S. O. Pearson and H. St. G. Anson, Demonstration of Some Electrical Properties of Neon-filled Lamps, Proceedings of the Physical Society of London, vol.34, no. 1 (December 1921), pp. 175–176 DOI 10.1088/1478-7814/34/1/435
• S. O. Pearson and H. St. G. Anson, The Neon Tube as a Means of Producing Intermittent Currents, Proceedings of the Physical Society of London, vol. 34, no. 1 (December 1921), pp. 204–212 DOI 10.1088/1478-7814/34/1/341
• C. L. Daugherty et al., G.E. Glow Lamp Manual, 2nd Ed., Cleveland, Ohio, General Electric, 1965, 14–19 p. (lire en ligne)