Effet électro-calorique

Figure 1 : Le cycle de refroidissement par effet magnétocalorique

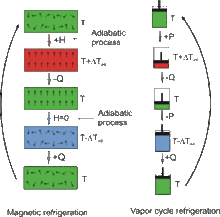
Les principes de fonctionnement de base de la réfrigération électro-calorique sont, en principe, analogues à ceux du refroidissement magnétique et par compression de vapeur. Ceux-ci sont constitués par le transport de chaleur d'une charge calorifique à l’environnement à travers un matériau électro-calorique, magnéto-calorique ou gaz qui est soumis à un cycle thermodynamique. Les cycles de réfrigération sont entraînés par la variation de l’entropie d’un matériau diélectrique polaire  lors d’une application ou annulation d’un champ électrique externe.

Le cycle de refroidissement électro-calorique est constitué de quatre  processus ; deux processus adiabatiques et deux processus isothermes:

1. Polarisation adiabatique : un matériau électro-calorique isolé est soumis à une augmentation brutale d’un champ électrique externe, qui entraîne une diminution de l’entropie des dipôles électriques. Comme le matériau est isolé de son environnement (conditions adiabatiques), il n'y a pas d'échange de chaleur, d’où le matériau s’échauffe et sa température augmente (T + ΔT).
2. Transfert de chaleur : Le matériau électro-calorique est mis en contact avec une source chaude. En maintenant un champ électrique constant le matériau expulse de la chaleur à la source chaude, d’où sa température diminue.
3. Dépolarisation adiabatique : le matériau électro-calorique est à nouveau isolé et le champ électrique appliqué est annulé. Cette annulation  du champ permet aux dipôles de s’orienter aléatoirement et d’augmenter l’entropie du système. Comme le matériau est isolé de son environnement (conditions adiabatiques), il n'y a pas d'échange de chaleur, d’où le matériau se refroidit et sa température diminue (T - ΔT).
4. Transfert entropique : En maintenant un champ électrique nul, le matériau électro-calorique est placé en contact avec une source froide. La chaleur migre de la source froide vers le réfrigérant qui l’absorbe et revient à sa température initiale[3].

Les matériaux utilisés pour de tels applications sont des ferroélectriques.Ces derniers présentent des constantes diélectriques et des indices de réfraction élevés. Ils possèdent également une polarisation spontanée (Ps) dans certains domaines de température et la direction de cette Ps peut être réorientée ou même renversée sous l’action d’un champ électrique externe. Leur polarisation décrit une hystérèse en fonction du champ électrique appliqué. Par analogie avec le comportement des ferromagnétiques sous champ magnétique, Müller leur donna le nom de ferroélectrique en 1935.

Figure 2 : Boucle d’hystérésis ferroélectrique typique

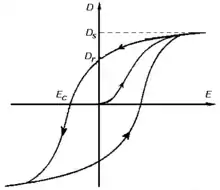
La figure 2 montre un cycle d’hystérésis typique d’un ferroélectrique avec D_s = la polarisation à saturation, D_r = la polarisation rémanente (à champ nul) et E_c = le champ coercitif. Le cycle d’hystérésis disparaît progressivement en s’approchant de la température de Curie. C'est la température à laquelle se produit la transition ferroélectrique-paraélectrique correspondant à un changement de structure qui a pour conséquence de supprimer la polarisation rémanente.

La partie décroissante de la courbe située dans la région paraélectrique suit une loi de type Curie-Weiss de formule :

${\displaystyle \chi \sim {\frac {c}{(T-T_{c})}}}$

Où c et T_c sont respectivement la constante et la température de Curie-Weiss.

Par conséquent :

• Si le matériau est chauffé au-dessus de sa température de Curie ou température de transition, sa polarisation spontanée disparaît. On dit alors que le matériau est dans son état paraélectrique.
• Si le matériau est refroidi en dessous de sa température de Curie, le caractère ferroélectrique réapparaît.

Au passage à T_c, deux phénomènes sont remarquables dans le matériau.

Premièrement, à cette transition, un pic très accentué de la constante diélectrique ε se manifeste.

Deuxièmement, le matériau subit un changement de structure à cette température. Au changement de structure, le matériau acquiert une élasticité maximale et devient très facilement polarisable.

Dans le cas des matériaux ferroélectriques, l’effet EC est étroitement lié à l’effet pyroélectrique. En effet, les effets pyroélectriques et électro-caloriques peuvent être considérés comme des effets réciproques. L’effet EC peut être utilisé pour la réfrigération tandis que l’effet pyroélectrique peut servir pour des capteurs de température/chaleur ou de la récupération d’énergie.

Le principe physique de l’effet électro-calorique est similaire à l'effet magnéto-calorique qui consiste à accroître l’écart de température. Toutefois, au lieu du processus d’aimantation ${\displaystyle (H)}$, le matériau électro-calorique est soumis à une polarisation/dépolarisation.

Afin d'étudier l'effet électro-calorique, la plupart des recherches reposent sur le calcul théorique de la relation de Maxwell pour estimer la valeur de ${\displaystyle \Delta T}$.

La relation de Maxwell est dérivée de deux fonctions (l'entropie (S), la température (T)) et (la polarisation (P), le champ électrique (E)) [Line and Glass, 1977]

${\displaystyle {(\partial S/\partial E)}_{T}={(\partial P/\partial T)}_{E}}$

Or,

${\displaystyle {(\partial T/\partial E)}_{S}=T/c_{p,E}{(\partial P/\partial T)}_{E}}$

Désormais, l'expression de la variation de température adiabatique des matériaux électro-calorique peut être obtenue par :

${\displaystyle \Delta T=-TV/c_{p,E}\int _{E_{1}}^{E_{2}}(\partial P/\partial T)_{E}dE}$

c étant la capacité thermique ou calorifique du matériau et V son volume.

Selon l'équation ci-dessus, pour aboutir à une large variation de ${\displaystyle \Delta T}$, le matériau diélectrique, doit avoir un coefficient pyroélectrique considérable sur un champ relativement élevé à un intervalle de température déterminé. Un large coefficient pyroélectrique d’un matériau ferroélectrique existe à la température de transition de phase. Par conséquent, cet effet est capable de décaler la température de transition suite à l’application d’un champ électrique externe.

L'effet pyroélectrique peut être décrit comme la dépendance en température de la polarisation spontanée d'un cristal[6]. Il s'agit de la variation de la polarisation d'un cristal lorsqu'il subit une variation de sa température.

Le matériau doit posséder une polarisation spontanée non nulle et de préférence dirigée perpendiculairement à la surface des électrodes.

Une faible variation de la température ${\displaystyle \mathrm {d} T}$ va produire un changement de la polarisation ${\displaystyle \mathrm {d} P}$. Si cette variation de température est effectuée dans un temps ${\displaystyle dt}$, la polarisation varie alors au cours du temps. Les charges d'espaces sont compensées par des charges libres présentes dans le matériau. Ce déplacement de charge génère un courant, le courant pyroélectrique. On aura, ${\displaystyle \mathrm {d} P/\mathrm {d} t}$ équivalent à un courant pyroélectrique ${\displaystyle i}$.

${\displaystyle i=(\mathrm {d} P/\mathrm {d} t)=(\mathrm {d} P/\mathrm {d} T)(\mathrm {d} T/\mathrm {d} t)}$

Le coefficient pyroélectrique décrit les changements du vecteur polarisation en réponse à un changement de température[7] :

${\displaystyle p_{i}={\frac {\partial P_{S,i}}{\partial T}}}$

où p_i (Cm^-2K^-1) est le vecteur du coefficient pyroélectrique.

Pour de faibles variations de ${\displaystyle \Delta T}$, ${\displaystyle \mathrm {d} P/\mathrm {d} T}$ peut être considéré comme une constante à cette température. Ainsi, le courant ne dépend que du taux de variation de la température. Si ce dernier est élevé, le courant i peut être détecté.

L’ECE a été observé pour la première fois par Kobeco et Kurtschatov[8] dans des matériaux ferroélectriques sel de Seignette ou sel de Rochelle. Bien que cet effet ait été découvert dès 1930, ce n’est qu’à partir des années 1960 que ses travaux se sont intensifiés. L’ECE des matériaux ferroélectriques (céramiques) et des monocristaux ont été étudiés[9] - [10] - [11], toutefois ils ont été abandonnés car les variations de températures restaient trop faibles (${\displaystyle \Delta T<2K}$ pour les céramiques et ${\displaystyle \Delta T<1K}$ pour les monocristaux) pour envisager une exploitation. En 2006, Michenko et al. ont découvert un ECE « géant » (${\displaystyle \Delta T=12K}$) sur une couche mince de PbZr_0.95Ti_0.05O₃ de 300 nm préparée par sol-gel sous un champ électrique de ${\displaystyle 780kV/cm}$ à 222 °C[12]. Cette découverte a revitalisé ce domaine et a incité de nombreuses études portant sur l'effet du champ électrique élevé sur la réponse pyroélectrique d'autres matériaux ferroélectriques. Les premiers travaux portent sur PZT et bien que cet alliage soit toujours en quête[13] - [14] d'autres cristaux de perovskite sont également intéressants, notamment PbMg_1/3Nb_2/3O₃ -x PbTiO₃[15] - [16], BTO[17] - [18], BaTiO₃ - SrTiO₃[19], et  les couches d’oxyde SrBi₂Ta₂O₉[20].

• Effet magnétocalorique
• Pyroélectricité