Dipôle oscillant

Le dipôle oscillant est un modèle intervenant en électromagnétisme décrivant les effets du mouvement oscillatoire d’une particule chargée aux alentours d’un point fixe. Il explique des phénomènes tels que la diffusion Rayleigh, le fonctionnement des antennes dipolaires, ou le rayonnement thermique.

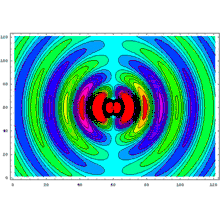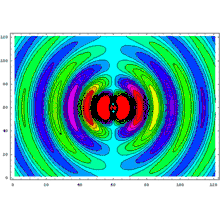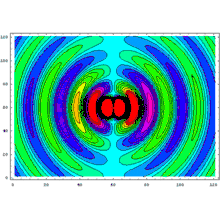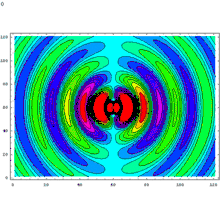
Évolution temporelle du champ électrique créé par un dipôle oscillant, l’oscillation se faisant selon l’axe vertical. On reconnaît près du centre une structure comparable à celle du dipôle statique ; en s’éloignant, il prend la forme d’une onde progressive.

Phénomène de rayonnement d’un dipôle

Une particule chargée est la source d’un champ électrique dépendant de sa position. Par conséquent, une particule en mouvement, telle qu’un électron se déplaçant librement autour d’un noyau d’atome, ou mis en mouvement par un champ forcé, engendre un champ électrique variable dans le temps, qui d’après les équations de Maxwell se propage sous la forme d’une onde électromagnétique.

En pratique, l’analyse de Fourier justifie qu’on ne s’intéresse qu’aux cas où le mouvement est sinusoïdal, les autres s’exprimant par superposition de solutions dans le cas sinusoïdal.

Description du modèle

Il s’agit en fait d’une adaptation du modèle du dipôle électrique classique, dans lequel le moment dipolaire est variable au cours du temps, sinusoïdal.

On considère un doublet de charges {q, -q} (où q peut être positif ou négatif). La charge q est fixe en O dans le référentiel d’étude. La charge -q est mobile, située en $M(t)$ avec ${\overrightarrow {OM(t)}}=z_{0}\cos(\omega t){\vec {u_{z}}}$ . Le système possède donc un moment dipolaire variable ${\vec {p}}(t)=\cos(\omega t){\vec {p_{0}}}$ avec ${\vec {p_{0}}}=z_{0}q{\vec {u_{z}}}$ . De plus, on suppose le mouvement de la particule non relativiste ( $z_{0}\omega$ faible devant $c$ ).

Par la suite, on cherchera uniquement à déterminer le champ à grande distance des charges, dans une acception détaillée ultérieurement. À plus faible distance du dipôle, en effet, la structure du champ est similaire à celle du dipôle (électrique ou magnétique) statique, variant linéairement avec le moment ${\vec {p}}$ .

On se place en coordonnées sphériques de centre O, d’axe $(O{\vec {z}})$ . La base de projection considérée est alors $({\vec {u_{r}}},{\vec {u_{\theta }}},{\vec {u_{\phi }}})$ , directe, avec ${\vec {u_{r}}}$ radial et ${\vec {u_{\theta }}}$ méridien.

Calcul du champ

Par linéarité des équations de Maxwell, le champ engendré est variable, harmonique de pulsation $\omega$ ; donc l’onde électromagnétique est de longueur d’onde $\lambda ={\frac {2\pi c'}{\omega }}$ , où $c'$ est la célérité de la lumière dans le milieu considéré ( $c$ dans le vide).

La structure du champ engendré est particulièrement complexe, vu le forçage imposé par le mouvement de la charge (le modèle de l’onde plane progressive harmonique n’est pas valable ici, sauf pour étudier la propagation à grande distance du champ engendré dans le milieu, en approximant les fronts d’onde par des plans tangents). On suppose donc que l’on étudie le champ à un rayon $r$ du point O grand devant $\lambda$ .

Les trois approximations se résument donc par :

$\lambda >>z_{0}$ : mouvement de M non relativiste
$r>>z_{0}$ : approximation dipolaire
$r>>\lambda$ : zone de rayonnement considérée grande devant la longueur d’onde.

Alors, en un point $P(r,\theta ,\phi )$ ( $\theta$ représentant la colatitude, c’est-à-dire l’angle ${\widehat {({\vec {u_{z}}},{\overrightarrow {OP}})}}$ ), les champs électrique et magnétique créés s’expriment :

{\vec {E}}(z,\theta ,t)=-{\frac {\mu _{0}}{4\pi r}}\omega ^{2}\|{\vec {p_{0}}}\|\sin \theta \cos \left[\omega \left(t-{\frac {r}{c'}}\right)\right]{\vec {u_{\theta }}}

{\vec {B}}(z,\theta ,t)=-{\frac {\mu _{0}}{4\pi rc'}}\omega ^{2}\|{\vec {p_{0}}}\|\sin \theta \cos \left[\omega \left(t-{\frac {r}{c'}}\right)\right]{\vec {u_{\phi }}}

Où $\mu _{0}$ est la perméabilité magnétique du vide.

Démonstration

On va faire la démonstration dans le vide[1]. Pour étudier un milieu quelconque et obtenir les relations ci-dessus, il suffit de remplacer c par c' dans toutes les expressions qui vont suivre.

On va utiliser le potentiel scalaire $\phi$ et le potentiel vecteur ${\overrightarrow {A}}$ pour faire notre étude. On a ${\overrightarrow {B}}={\overrightarrow {\nabla }}\wedge {\overrightarrow {A}}$ et ${\overrightarrow {E}}=-{\overrightarrow {\nabla }}\phi -{\frac {\partial {\overrightarrow {A}}}{\partial t}}$ .

On utilisera aussi la jauge de Lorentz :

   ${\overrightarrow {\nabla }}\cdot {\overrightarrow {A}}+\mu _{0}\epsilon _{0}{\frac {\partial \phi }{\partial t}}=0$

On a ainsi : ${\overrightarrow {\nabla }}\wedge {\overrightarrow {B}}={\overrightarrow {\nabla }}\wedge ({\overrightarrow {\nabla }}\wedge {\overrightarrow {A}})={\overrightarrow {\nabla }}({\overrightarrow {\nabla }}\cdot {\overrightarrow {A}})-{\overrightarrow {\nabla }}^{2}{\overrightarrow {A}}=\mu _{0}{\overrightarrow {j}}+\mu _{0}\epsilon _{0}\left(-{\overrightarrow {\nabla }}{\frac {\partial \phi }{\partial t}}-{\frac {\partial ^{2}{\overrightarrow {A}}}{\partial t^{2}}}\right)$

Donc d'après la jauge de Lorentz : ${\overrightarrow {\nabla }}\left({\overrightarrow {\nabla }}\cdot {\overrightarrow {A}}+\mu _{0}\epsilon _{0}{\frac {\partial \phi }{\partial t}}\right)={\overrightarrow {\nabla }}^{2}{\overrightarrow {A}}-\mu _{0}\epsilon _{0}{\frac {\partial ^{2}{\overrightarrow {A}}}{\partial t^{2}}}+\mu _{0}{\overrightarrow {j}}=0$

Le potentiel vecteur vérifie donc :

   $\Box {\overrightarrow {A}}={\overrightarrow {\nabla }}^{2}{\overrightarrow {A}}-{\frac {1}{c^{2}}}{\frac {\partial ^{2}{\overrightarrow {A}}}{\partial t^{2}}}=-\mu _{0}{\overrightarrow {j}}$

De même, on montre que : ${\overrightarrow {\nabla }}\cdot {\overrightarrow {E}}={\overrightarrow {\nabla }}\cdot \left(-{\overrightarrow {\nabla }}\phi -{\frac {\partial {\overrightarrow {A}}}{\partial t}}\right)={\frac {\rho }{\epsilon _{0}}}$

Et avec la Jauge de Lorentz : ${\overrightarrow {-\nabla }}^{2}\phi +\mu _{0}\epsilon _{0}{\frac {\partial ^{2}\phi }{\partial t^{2}}}={\frac {\rho }{\epsilon _{0}}}$

Donc le potentiel scalaire vérifie :

    $\Box \phi ={\overrightarrow {\nabla }}^{2}\phi -{\frac {1}{c^{2}}}{\frac {\partial ^{2}\phi }{\partial t^{2}}}=-{\frac {\rho }{\epsilon _{0}}}$

Or, on sait comment résoudre ces équations. Il faut utiliser les formules des potentiels retardés. En effet, les effets de ${\overrightarrow {j}}$ et de $\rho$ ne sont pas instantanés.

On a donc :

   ${\overrightarrow {A}}({\overrightarrow {r}},t)={\frac {\mu _{0}}{4\pi }}\int {\frac {{\overrightarrow {j}}({\overrightarrow {r'}},t')}{|{\overrightarrow {r}}-{\overrightarrow {r'}}|}}d{\overrightarrow {r'}}$

et :

  $V({\overrightarrow {r}},t)={\frac {1}{4\pi \epsilon _{0}}}\int {\frac {\rho ({\overrightarrow {r'}},t')}{|{\overrightarrow {r}}-{\overrightarrow {r'}}|}}d{\overrightarrow {r'}}$

où $t'=t-{\frac {|{\overrightarrow {r}}-{\overrightarrow {r'}}|}{c}}$ .

Commençons par calculer ${\overrightarrow {A}}$ .

Au vu de notre système, on peut écrire : ${\overrightarrow {A}}({\overrightarrow {r}},t)={\frac {-\mu _{0}}{4\pi }}{\frac {q{\overrightarrow {v}}(t-{\frac {|{\overrightarrow {r}}-{\overrightarrow {OM}}|}{c}})}{|{\overrightarrow {r}}-{\overrightarrow {OM}}|}}$ où ${\overrightarrow {v}}={\dot {\overrightarrow {OM}}}$ .

Or, la dérivée temporelle du moment dipolaire peut se réécrire ${\dot {\overrightarrow {p}}}=-q{\overrightarrow {v}}$ .

Donc le potentiel vecteur devient : ${\overrightarrow {A}}({\overrightarrow {r}},t)={\frac {\mu _{0}}{4\pi }}{\frac {{\dot {\overrightarrow {p}}}(t-{\frac {|{\overrightarrow {r}}-{\overrightarrow {OM}}|}{c}})}{|{\overrightarrow {r}}-{\overrightarrow {OM}}|}}$

Utilisons l'approximation dipolaire, qui nous permet d'écrire $|{\overrightarrow {r}}|\gg |{\overrightarrow {OM}}|$ , donc $|{\overrightarrow {r}}-{\overrightarrow {OM}}|\sim |{\overrightarrow {r}}|=r$ . Utilisons de plus l'hypothèse non relativiste, qui donne $\lambda \gg z_{0}$ , et qui fait que l'on peut négliger le décalage temporel entre $t-{\frac {|{\overrightarrow {r}}-{\overrightarrow {OM}}|}{c}}$ et $t-{\frac {r}{c}}$ (de l'ordre de ${\frac {z_{0}}{c}}\ll {\frac {\lambda }{c}}$ ), et donc écrire : ${\dot {\overrightarrow {p}}}(t-{\frac {|{\overrightarrow {r}}-{\overrightarrow {OM}}|}{c}})\sim {\dot {\overrightarrow {p}}}(t-{\frac {r}{c}})$ .

Ainsi

${\overrightarrow {A}}({\overrightarrow {r}},t)={\frac {\mu _{0}}{4\pi }}{\frac {{\dot {\overrightarrow {p}}}(t-{\frac {r}{c}})}{r}}$

On peut facilement calculer le champ magnétique grâce à ${\overrightarrow {B}}={\overrightarrow {\nabla }}\wedge {\overrightarrow {A}}$ :

${\overrightarrow {B}}({\overrightarrow {r}},t)={\frac {\mu _{0}}{4\pi }}\sin {\theta }\left({\frac {{\dot {p}}(t-{\frac {r}{c}})}{r^{2}}}+{\frac {{\ddot {p}}(t-{\frac {r}{c}})}{rc}}\right){\overrightarrow {e_{\phi }}}$

Pour calculer le champ électrique, on peut soit calculer le potentiel scalaire, soit utiliser l'équation de Maxwell-Ampère.

On obtient :

${\overrightarrow {E}}({\overrightarrow {r}},t)={\frac {1}{4\pi \epsilon _{0}}}\left(2\cos {\theta }\left[{\frac {1}{r^{2}c}}{\dot {p}}(t-{\frac {r}{c}})+{\frac {1}{r^{3}}}p(t-{\frac {r}{c}})\right]{\overrightarrow {e_{r}}}+\sin {\theta }\left[{\frac {p}{r^{3}}}+{\frac {{\dot {p}}(t-{\frac {r}{c}})}{r^{2}c}}+{\frac {{\ddot {p}}(t-{\frac {r}{c}})}{rc^{2}}}\right]{\overrightarrow {e_{\theta }}}\right)$

On va simplifier ces expressions en se plaçant dans la zone de rayonnement, qui est telle que $r\gg \lambda$ , ce qui revient à ne garder que les termes ayant la puissance de $r$ la plus basse (car en ordre de grandeur, ${\frac {\dot {p}}{r^{2}c}}\sim 2\pi {\frac {p}{r^{3}}}{\frac {r}{\lambda }}$ et ${\frac {\ddot {p}}{rc^{2}}}\sim 4\pi ^{2}{\frac {p}{r^{3}}}\left({\frac {r}{\lambda }}\right)^{2}$ ).

On obtient donc :

${\overrightarrow {E}}({\overrightarrow {r}},t)={\frac {\sin {\theta }}{4\pi \epsilon _{0}{rc^{2}}}}{\ddot {p}}(t-{\frac {r}{c}}){\overrightarrow {e_{\theta }}}$ et : ${\overrightarrow {B}}({\overrightarrow {r}},t)={\frac {\mu _{0}\sin {\theta }}{4\pi {rc}}}{\ddot {p}}(t-{\frac {r}{c}}){\overrightarrow {e_{\phi }}}$

Pour obtenir les expressions ci-dessus, il suffit d'écrire les dérivées secondes du moment dipolaire.

On reconnaît la structure d’une onde sphérique progressive de pulsation $\omega$ et de module d’onde ${\frac {\omega }{c'}}$ . Elle est de plus anisotrope, le champ étant maximal dans le plan équatorial, et nul selon l’axe du dipôle.

Applications

Photographie d’une antenne pliée

Ce modèle est à l’origine du fonctionnement des antennes dipolaires émettrices : on considère chaque élément de longueur métallique traversé par un courant variable comme un dipôle oscillant élémentaire ; le champ total créé est alors l’intégrale sur la longueur de l’antenne des champs engendrés par les dipôles élémentaires.

Il explique aussi le rayonnement des particules chargées accélérées, et se généralise par le modèle du rayonnement dipolaire électrique et celui du rayonnement dipolaire magnétique.

Notes et références