Construction de l'angle moitié
Soit un angle de sommet O dont on souhaite construire l'angle moitié à l'aide de la règle et du compas, et sans utiliser le rapporteur.
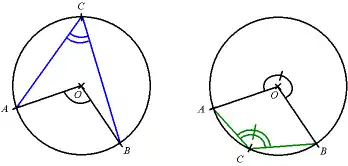
Il suffit de tracer un cercle de centre O et de rayon quelconque qui coupe les demi-droites de l'angle en A et B, puis de prendre un point C sur le cercle ; l'angle moitié sera ACB. Il faut prendre le point C sur la bonne partie du cercle, sinon on obtiendrait le supplémentaire de l'angle moitié.
Pour approfondir
On pourrait souhaiter la généralisation de ce type de constructions, diviser un angle en 3, 5, 7 etc., mais il a été démontré que la trisection de l'angle fait partie des problèmes impossibles à résoudre à la règle et au compas.
Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.