Construction d'une parabole tangente par tangente
Exemples

Une propriété tangentielle des coniques est la suivante: si, sur deux axes, on établit une correspondance homographique entre les points de l'un et les points de l'autre, toute droite joignant un point de l'un à son image sur l'autre est tangente à une conique. Ceci est valable pour les coniques particulières que sont les paraboles.
- Dans le premier exemple, la conique est la parabole y=x² qu'on appuie sur deux droites: la première est l'axe des abscisses, la seconde est la tangente à la parabole au point de coordonnées (2 , 4) ; une tangente variable, au point de la parabole ( 2t , 4t²), coupe ces deux droites aux distances (par rapport à leur coude) respectives et , le point B ayant comme coordonnées [(t+1), 4*t]. En éliminant le paramètre t entre ces deux équations nous obtenons la relation : , qui n'est qu'un cas particulier et dégénéré de la fonction homographique : , dans laquelle c=0, d=1, b=, a= .
- Remarque: une telle construction tangentielle d'une parabole ne donne pas les points de contact entre la parabole et ses tangentes.
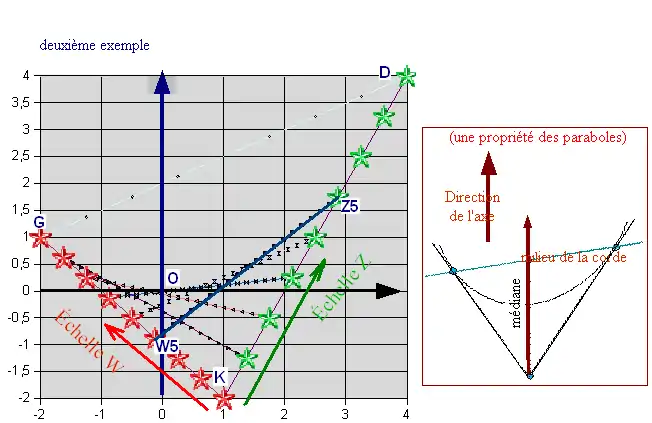
- Le deuxième exemple illustre la construction des tangentes en s'appuyant sur 2 tangentes particulières KG et KD. Ici la parabole est y=(1/4)* x², le point K est (1;-2) à partir duquel on mène deux tangentes d'équations y=-x-1 et y=2x-4; les points de contact G et D sont de coordonnées respectives (-2; 1) et (4;4). La méthode consiste à créer deux "échelles" WK et KZ graduées en n subdivisions égales, 8 par exemple, à relier les points Wi et Zi correspondants, la droite ainsi obtenue est un tangente à la parabole, mais on ne connaît pas le point de contact. Si les 8 points de W et Z ne suffisent pas, on peut augmenter la finesse des subdivisions, 20, 50 ou 100 par exemple.
Explication de cette méthode
La propriété de la parabole utilisée ici est que lorsqu'on considère le triangle formé par deux tangentes et la corde entre les points de contacts, la médiane issue du point d'intersection des tangentes est parallèle à l'axe de la parabole.
- Si on applique cette propriété à trois tangentes GK, WZ et DK, tangentes aux points G, T et D, alors W' est le milieu de GT, Z' est le milieu de TD et K' est le milieu de GD. D'où l'on déduit que W" est le milieu de GT' et Z" le milieu de T'D.
- En examinant ce qui se passe sur la corde GD, on en déduit qu'une translation de vecteur GK' transforme G en K', W" en Z" et K' en D. D'où l'égalité des rapports GW"/GK' et K'Z"/K'D.
- Deux applications du théorème de Thalès montrent que ce rapport est aussi égal à GW/GK et à KZ/KD.
- L'égalité GW / GK= KZ / KD montre que W et Z sont les points de subdivision correspondants sur les deux "échelles" GK et KD, ce qui explique la méthode précédente.

Fonction homographique mise en jeu
Dans l'ellipse y=(1/4)* x², si W a pour abscisse w, alors la longueur GW mesure (1-w)√2, la longueur KZ mesure (2+w)√5, l'élimination de Z entre les deux conduit à la correspondance entre les points des deux échelles: KZ = √5(3-GW/√2), qui n'est qu'un cas particulier et dégénéré de la fonction homographique
- Ceci illustre de manière analytique la propriété générale selon laquelle une conique est engendrée tangentiellement par les droites joignant deux alignements de points en correspondance homographique, ici les alignements W et Z.
Explication par la géométrie projective pure
La correspondance homographique entre les alignements W et Z peut être construite d'une manière graphique, sans calculs analytiques, grâce à un parallélogramme variable KWHZ. Soit la transformation T définie comme la succession de 2 transformations de points projectives unidimensionnelles; la première est la perspective de centre Zinfini de la droite w sur la droite h=corde GD; la seconde est la perspective de centre Winfini de la droite h sur la droite z.
- Le point G est d'abord transformé en G puis en K, d'où la droite GK qui est bien tangente à la parabole.
- Le point K est d'abord transformé en D puis en D, d'où la droite KD qui est bien tangente à la parabole.
- Le point Winfini est d'abord transformé en Hinfini puis en Zinfini, d'où la droite (Winfini-Zinfini)=droite de l'infini qui est tangente à toute parabole.
- Le théorème fondamental de la géométrie projective nous assure que T est définie de manière unique par ces trois transformés de points. Si nous appliquons maintenant cette transformation au point variable W, il est d'abord transformé en H puis en Z, d'où la tangente variable WZ.
- Or les triangles GWH et HZD sont homothétiques au triangle GKD, donc W" est le milieu de GH, il était déjà le milieu de GT', donc H et T' sont le même point. Les deux méthodes proposées sont donc équivalentes.
Articulation entre la géométrie projective et la géométrie euclidienne
Géométrie projective. Cet exemple en géométrie projective se résume à tracer d'autres tangentes à une conique ayant 3 tangentes (la droite de l'infini, GK et KD), et passant par les 2 points G et D, 5 éléments au total. Elles se construisent par les alignements W et Z reliés par l'homographie T. D'après les théorèmes de la géométrie projective tout ce qu'on peut affirmer est que les droites ainsi créées sont tangentes à une conique. Dans cette géométrie l'homographie se réalise uniquement par le dessin.
- Géométrie métrique. L'homographie se réalise par des mesures de longueurs et des calculs analytiques. L'utilisation des "graduations" de longueurs W et Z reliées par une fonction homographique est trop luxueuse pour une parabole, mais a été mentionnée comme conforme au cas d'application générale pour construire une conique.
- Géométrie affine. Pour parler d'une parabole, nous avons besoin de notions simplement affines, c’est-à-dire de parallélogrammes (autrement dit de droites parallèles et milieux-affines de segments), ce qui est bien le cas lors de deux variantes
- dans la dernière construction mentionnée, avec l'intervention d'un parallélogramme variable, KWHZ, des deux faisceaux parallèles Winfini et Zinfini ainsi que l'utilisation des milieux-affines W', W", K', Z' et Z".
- dans la première construction, on utilise deux "échelles" WK et KZ graduées en n subdivisions égales, en se contentant de choisir n égal à une puissance de 2. De telles subdivisions sont constructibles en trouvant autant de fois que nécessaire des milieux de segments, opération que l'on sait faire dans un plan affine, voir Constructions du milieu d'un segment, on utilise des parallélogrammes.






