Conjecture de Pólya

La conjecture de Pólya énonce que pour tout entier n supérieur à 2, si l'on partitionne les entiers naturels inférieurs ou égaux à n (en ne comptant pas 0) entre ceux qui ont un nombre impair de facteurs premiers et ceux qui en ont un nombre pair, alors le premier ensemble a plus (ou autant) d'éléments que le second. Il faut noter que les facteurs premiers sont comptés autant de fois qu'ils sont répétés. Ainsi, 24 = 2³ × 3¹ a 3 + 1 = 4 facteurs premiers, alors que 30 = 2 × 3 × 5 a 3 facteurs premiers.

De façon équivalente, la conjecture peut être formulée avec la fonction de Liouville de la façon suivante :

${\displaystyle L(n)=\sum _{k=1}^{n}\lambda (k)\leq 0}$

pour tout n > 1. Ici, λ(k) = (−1)^Ω(k) vaut 1 si le nombre de facteurs premiers de l'entier k est pair, et -1 s'il est impair. La fonction Ω compte le nombre total de facteurs premiers d'un entier.

La conjecture de Pólya a été réfutée par C. Brian Haselgrove en 1958. Il a montré qu'elle avait un contre-exemple, qu'il a estimé à environ 1,845 × 10³⁶¹[2].

Un contre-exemple explicite, pour n = 906 180 359, a été donné par R. Sherman Lehman en 1960[3] ; le plus petit contre-exemple est n = 906 150 257, trouvé par Minoru Tanaka en 1980[4].

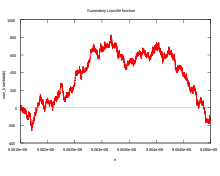
La conjecture de Pólya est en défaut pour la plupart des valeurs de n dans la région 906 150 257 ≤ n ≤ 906 488 079. Dans cette zone, la fonction de Liouville atteint une valeur maximale de 829 en n = 906 316 571.

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Pólya conjecture » (voir la liste des auteurs).