Composantes d'une force
En physique, les composantes d'une force sont les projections d'une force en vecteurs orthogonaux selon un système d'axes donné. Ces projections permettent notamment d'effectuer des opérations mathématiques avec la force impliquée. Ainsi, par exemple, pour étudier l'effet d'une force sur un corps, il est parfois plus simple de décomposer cette force en plusieurs composantes que l'on étudiera séparément.
Inversement, la somme des composantes d'une ou de plusieurs forces agissant sur un corps donne une force résultante.
Composantes vectorielles
Une force étant caractérisée par son intensité et par la direction vers laquelle elle agit, elle peut, par conséquent, être représentée sous forme d'un vecteur puisqu'elle en possède les deux caractéristiques fondamentales : une grandeur et une orientation[1]. Ce type de vecteur peut être décomposé de différentes façons.
Composantes cartésiennes
Il est également possible de décomposer une force en ses composantes cartésiennes. Ces composantes sont obtenues par la projection de la force sur les axes du plan où elle se trouve[2].
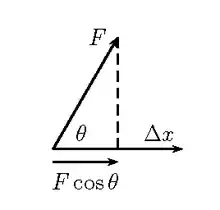
Ainsi, si on étudie une force dans un plan xy, il est possible de déterminer ses composantes en x (Fx) et en y (Fy) à partir de la grandeur F à l'aide des relations suivantes.
où θ est l'angle d'élévation de la force par rapport à l'axe positif des abscisses.Il faut ajouter les 2 composantes pour trouver l'expression vectorielle de la force.
La relation entre la norme de la force étudiée et celles des composantes est donnée par le théorème de Pythagore[3].
Dans un plan xyz, les composantes cartésiennes d'une force se calculent avec le cosinus de l'angle respectif la séparant de chaque axe pour déterminer les normes des composantes de chaque plan. La norme de cette force est obtenue de la même manière qu'en deux dimensions, seulement que, dans ce cas, il faut tenir compte de la norme des trois projections[4].
Exemples
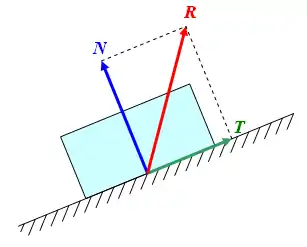
Plan incliné

Le cas d'un corps situé sur un plan incliné est un exemple classique faisant intervenir les composantes d'une force. Dans cette situation, les forces concernées sont le poids (), le poids apparent () et le frottement ().
Mouvement de rotation
La projection en plusieurs composantes prend un intérêt tout particulier avec l'utilisation d'un repère de Frenet. En effet, on sait exprimer facilement dans ce repère la vitesse et l'accélération d'un objet en rotation circulaire autour d'un point en fonction du rayon du mouvement et de la variation de l'angle. Dans le cas d'un mouvement à force centrale, en particulier, la force s'appliquant à l'objet n'ayant pas de composante tangentielle, l'expression se simplifie.
Notes et références
- Kane et Sternheim 1986, p. 29
- Benson 2009, p. 25
- Benson 2009, p. 27
- Benson 2009, p. 28
Annexes
Articles connexes
Bibliographie
![]() : document utilisé comme source pour la rédaction de cet article.
: document utilisé comme source pour la rédaction de cet article.
 Harris Benson (trad. Marc Séguin, Benoît Villeneuve, Bernard Marcheterre et Richard Gagnon), Physique 1 Mécanique, Édition du Renouveau Pédagogique, , 4e éd., 465 p.
Harris Benson (trad. Marc Séguin, Benoît Villeneuve, Bernard Marcheterre et Richard Gagnon), Physique 1 Mécanique, Édition du Renouveau Pédagogique, , 4e éd., 465 p. Joseph W. Kane et Morton M. Sternheim (adaptation Michel Delmelle), Physique, Interédition, , 775 p.
Joseph W. Kane et Morton M. Sternheim (adaptation Michel Delmelle), Physique, Interédition, , 775 p.









