Coloration forte

En théorie des graphes, une coloration forte est une coloration de graphe dans laquelle chaque couleur apparaît exactement une fois dans chaque partition, avec une partition des sommets en sous-ensembles (disjoints) de même taille.

Cette échelle de Möbius est fortement 4-colorable. Il y a 35 partitions de taille 4, mais seules ces 7 partitions sont topologiquement distinctes.

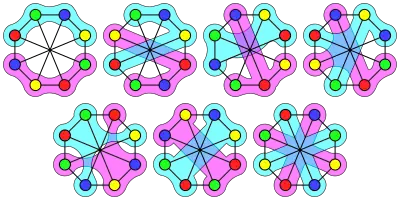
Lorsque l'ordre du graphe G n'est pas divisible par k, on ajoute des sommets isolés à G juste assez pour rendre l'ordre de ce nouveau graphe G' divisible par k. Dans ce cas, une forte coloration de G' moins les sommets isolés ajoutés précédemment est considérée comme une forte coloration de G. Un graphe est fortement k-colorable si, pour chaque partition des sommets en deux ensembles de taille k, il admet une coloration forte.

L' indice chromatique fort sχ(G) d'un graphe G est le plus petit nombre k tel que G est fortement k-colorable. Un graphe est fortement k-chromatique s'il a pour indice chromatique fort k.

Certaines propriétés de sx(G):

1. sχ(G) > Δ(G).
2. sχ(G) ≤ 3 Δ(G) - 1 (Haxell)
3. Asymptotiquement, sχ(G) ≤ 11 Δ(G) / 4 + o(Δ(G)). (Haxell)

Ici Δ(G) est le degré maximal.

La notion d'indice chromatique fort a été introduite indépendamment par Noga Alon (1988) et Michael Fellows (1990).