Bonnet turc
Le bonnet turc, Turk's head knot en anglais, est un nœud souvent considéré comme décoratif, mais qui peut servir également de repère (le « zéro » sur une barre à roue), ou de protection, par exemple contre le frottement d'un bout sur un espar ou pour améliorer une prise en main.

| Catégorie |
|---|
Nouage
Noué avec un seul brin, ce nœud n'est pas une tresse. Le bonnet turc est un nœud cylindrique avec une alternance stricte de "Dessus et de Dessous". Il existe une infinité de bonnets turcs qui sont désignés en fonction du nombre de spires et du nombre de ganses qui le composent ; ainsi on parlera par exemple : d'un bonnet turc à 3 spires et 5 ganses (un "3 × 5"), bonnet turc étroit, d'un bonnet turc à 4 spires et 3 ganses, (un "4 × 3"), bonnet turc carré, ou d'un 19 spires et 4 ganses (un "19 × 4"), bonnet turc large.
Ce nœud est généralement doublé, triplé ou plus pour avoir davantage de volume.
Ci-dessous, la confection d'un bonnet turc 3 × 4 d'après un manuel de Verrill Hyatt de 1919.
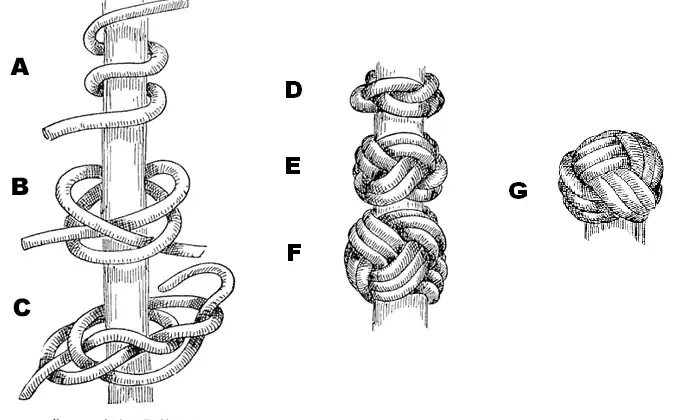
Usage
- Protection contre les chocs et usures (ragage) sur un navire.
- Décoration.
- On peut les employer pour gainer un manche d'outil ou de différents objets pour en améliorer la prise en main (barre franche).
- Certains bonnets turcs, plutôt que d'être utilisés autour d'un objet, d'un espar ou d'un cordage, peuvent être utilisés à plat en protection (autour de la fixation d'une poulie sur un pont) ou en décoration (centre de table).
- Ce nœud est également utilisé par les scouts pour confectionner leur bague de foulard, généralement un 4 × 3 ou un 5 × 3, doublé ou triplé.
Galerie
 Bonnet turc 3 spires et 4 ganses doublé
Bonnet turc 3 spires et 4 ganses doublé Bonnet turc 3 spires et 4 ganses quadruplé et mis à plat, protection de pont ou centre de table décoratif.
Bonnet turc 3 spires et 4 ganses quadruplé et mis à plat, protection de pont ou centre de table décoratif. Un bonnet turc 3 spires et 10 ganses (bonnet turc étroit) doublé et mis à plat.
Un bonnet turc 3 spires et 10 ganses (bonnet turc étroit) doublé et mis à plat. Bague 3 spires et 4 ganses triplé, briquet 6 spires et 5 ganses triplé.
Bague 3 spires et 4 ganses triplé, briquet 6 spires et 5 ganses triplé. Bonnet turc à chevrons.
Bonnet turc à chevrons. Bonnet turc 7x11 (bonnet turc large) triplé, ici pour améliorer la prise en main de cette lampe torche Maglite.
Bonnet turc 7x11 (bonnet turc large) triplé, ici pour améliorer la prise en main de cette lampe torche Maglite.
Lien externe
Robert Ferréol, « Étude mathématique des bonnets turcs », sur Encyclopédie des formes mathématiques remarquables