Automate séquentiel
En informatique théorique, et notamment en théorie des automates, un automate séquentiel est un automate fini déterministe avec sorties. C'est un cas particulier d'un transducteur fini, où l'automate des entrées est déterministe. Une sous-famille des automates séquentiels est celle des automates séquentiels dits purs, où certaines modalités de calcul sont simplifiées. Lorsque de plus les sorties sont des lettres, un automate séquentiel est un automate de Mealy. Les transductions rationnelles réalisées par les automates séquentiels sont des fonctions (partielles) appelées fonctions séquentielles.
Définition informelle
Les automates séquentiels sont des automates finis déterministes qui produisent un mot de sortie. Un tel automate peut réaliser certaines transformations comme l’addition des entiers dans une certaine représentation, la multiplication par une constante ou divers codages et décodages.
Dans un automate séquentiel, comme dans une transducteur fini, les transitions sont étiquetées par des couples formés d’une lettre d'entrée et d’un mot de sortie. De plus l’état initial est étiqueté par un mot appelé le « préfixe initial » et chaque état porte de plus un mot qui est la valeur d'une « fonction terminale ». Le mot de sortie calculé pour un mot d’entrée s’obtient en lisant l’entrée depuis l’état initial et en produisant les sorties spécifiées par les transitions ; le mot formé par ces sorties est préfixé par le préfixe initial et suffixé par le mot donné pour l’état final atteint. Si la fonction terminale n'est pas définie pour cet état, aucune sortie n'est produite. Lorsque le préfixe initial et la fonction terminale sont triviales, l'automate est un automate séquentiel pur.
La fonction réalisée par un automate séquentiel est une fonction séquentielle. C'est un cas particulier de transduction rationnelle fonctionnelle. Lorsque l'automate sous-jacent est pur, la fonction réalisée est elle-même dite pure. Un automate séquentiel pur est un transducteur fini particulier : l’automate d'entrée sous-jacent est déterministe (mais pas nécessairement complet).
Exemple
Voici un exemple[1] pour éclairer le concept :

Cet automate a deux états ; l'état initial 1 a pour préfixe initial 11 ; la fonction terminale associe à l'état 1 le mot vide et à l'état 2 le mot 00. L'automate est déterministe et incomplet. La lecture du mot fait passer l'automate progressivement par les états 1,2,2,1 et produit les sorties : ; préfixée de 11, concaténées et suivies de 00, on obtient 110100100. La fonction réalisée par cet automate prend donc, pour le d'entrée , la valeur 110100100.
Définition
On définit d'abord un automate séquentiel pur[1] : un automate séquentiel pur est un tuple
où
- est un ensemble fini d'états,
- et sont les alphabets finis d'entrée et de sortie respectivement
- est l'état initial
- est la fonction partielle de transition
- est la fonction partielle de sortie
Les fonctions de transition et de sortie ont le même domaine de définition . On note l'absence de définition explicite d'états terminaux : un état est terminal s'il appartient au domaine de définition de la fonction de sortie
Un automate séquentiel est un tuple où est un automate séquentiel pur, m∈B∗ est le préfixe initial et est une fonction (partielle), appelée la fonction terminale.
La fonction de transition s’étend à en posant et, si et sont définies,
- .
La fonction de sortie s’étend à en posant et, si et sont définies,
- .
Cette dernière formule exprime simplement que, lors d'un cheminement dans l'automate, les sorties des transitions sont concaténées à la suite.
La fonction réalisée par un automate séquentiel pur est l'application (partielle) définie sur un mot si est définie, et qui prend la valeur
- . La fonction réalisée par un automate séquentiel pur est l'application (partielle)
définie sur un mot si est définie, et qui prend la valeur
- .
La valeur est donc le mot obtenu en concaténant le préfixe initial avec le mot produit dans l'automate pur, suivi de la valeur que prend la fonction terminale sur l'état d'arrivée (si cet état est atteint et si la fonction terminale est définie sur cet état).
La fonction réalisée par un automate séquentiel pur est appelée une fonction séquentielle pure. De même, la fonction réalisée par un automate séquentiel est appelée une fonction séquentielle.
Exemples
Exemples de fonctions séquentielles pures
- Morphisme
Tout morphisme peut être réalisé par un automate séquentiel pur à un seul état
- Remplacer une suite d'espaces par un seul espace
Par exemple, le mot ab———a—a est transformé en ab—a—a.
- Codage et décodage

Un codage défini par
comme tout morphisme, peut être réalisé par un automate séquentiel pur à un seul état. Le décodage est possible par un automate séquentiel pur si le code est préfixe, et plus précisément le décodage est une fonction séquentielle si et seulement si le code est à délai de déchiffrage fini[2]. Ici, l'ensemble est bien un code préfixe et un automate séquentiel pur de décodage existe, donné sur la figure ci-contre[1]. Pour le mot
- 010101101000101101010110
le décodage donne
Exemples de fonctions séquentielles
- Fonction +1
Une fonction qui ajoute 1 au nombre écrit en binaire retournée (bit le plus faible à gauche), par exemple
- , et aussi .
- Additionneur binaire

Un additionneur binaire prend en argument deux entiers naturels écrits en binaire, et produit en sortie la suite binaire qui représente la somme des deux entiers. Les nombres en arguments sont écrits comme couples de bits, donc sur l'alphabet produit , le plus court des deux nombres binaires est éventuellement complété par des 0 ; l'écriture se fait avec le bit de plus petit poids à gauche[3]. Les deux états 0 et 1 de l'automate correspondent à l'absence respectivement la présence d'une retenue. Par exemple, pour , dont l'écriture binaire est 01101 et , dont l'écriture binaire complétée par un 0 à droite est 10110, la lecture des couples (0,1)(1,0)(1,1)(0,1)(1,0) fait passer successivement par les états 0,0,0,1,1,1; les lettres émises sont 1,1,0,0,0; la fonction de sortie fournit un 1 supplémentaire correspondant à la retenue, de sorte que le mot obtenu est 110001 qui est l'écriture binaire de .
Autres exemples
- Multiplicateur par une constante, division avec reste par une constante
- Multiplication ou division de polynômes à coefficients dans un corps fini par un autre fixe
- Analyse lexicale
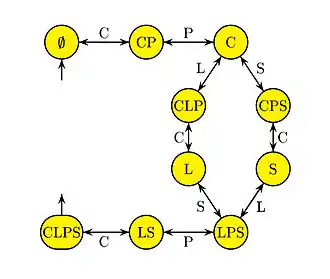
- Modélisation de certains systèmes finis, comme la fameuse devinette du transport d'une chèvre, d'un chou et d'un loup.
Caractérisations des fonctions séquentielles
La caractérisation des fonctions séquentielles et fonctions séquentielles pures fait appel à des notions topologiques :
- La distance géodésique[1] ou distance préfixe[4] entre deux mots u et v est le nombre où est le plus long préfixe commun de et . Si on voit les mots comme étiquetant les arcs des chemins dans un arbre, le plus long préfixe commun et plus petit ancêtre commun (« least common ancestor » ou « lca » en anglais). Par exemple, pour et , on a , donc . C'est la somme des longueurs des suffixes de et qui restent quand on leur enlève leur préfixe commun.
- Une fonction est lipschitzienne s’il existe un tel que pour tout
Théorème (Ginsburg et Rose (1966)[5]) — Une fonction est une fonction séquentielle pure si et seulement si
- est lipschitzienne ;
- préserve les préfixe (si est préfixe de , alors est préfixe de ;
- préserve les langages réguliers.
Théorème (Choffrut (1979)[6]) — Une fonction dont le domaine de définition est préfixiel (fermé par préfixe) est une fonction séquentielle si et seulement si
- est lipschitzienne ;
- préserve les langages réguliers.
Un autre résultat caractérise des fonctions séquentielles parmi les fonctions rationnelles, c'est-à-dire les transductions rationnelles qui sont des fonctions. Pour cela, on dit qu'une fonction est uniformément bornée si, pour tout entier , il existe un entier tel que pour tous dans le domaine de définition de .
Théorème[4] — Soit une fonction rationnelle. Les conditions suivantes sont équivalentes :
- est séquentielle ;
- est lipschitzienne ;
- est uniformément bornée.
Propriétés
Les fonctions séquentielles (pures) sont fermées par composition. En d'autres termes, le composé de deux fonctions séquentielles (pures) est encore une fonction séquentielle (pure).
Il est décidable si une fonction rationnelle est séquentielle (pure).
Note historique
Le terme de sequential transducer apparaît déjà dans les travaux de Seymour Ginsburg sous le nom de « generalized sequential machine (gsm) »[7]. Un long chapitre est consacré à ces machines et fonctions dans le traité de Samuel Eilenberg. Marcel-Paul Schützenberger[8] appelle sous-séquentielle une fonction séquentielle, et séquentielle une fonction pure, et ne s'écarte ainsi pas des définitions de ses prédécesseurs. Jacques Sakarovitch[4] emploie la terminologie utilisée ici, reprise à sa suite aussi par Jean-Éric Pin[3] - [2].
Notes et références
Bibliographie
- [Pin 2006] Jean-Eric Pin, chap. I/9 « Algorithmique et Programmation. Automates finis », dans Jacky Akoka et Isabelle Comyn-Wattiau (éditeurs), Encyclopédie de l’informatique et des systèmes d’information, Paris, Vuibert, (ISBN 978-2711748464, HAL hal-00143940/document), p. 966-976
- [Pin 2013] Jean-Éric Pin, « Petit cours sur les fonctions séquentielles », Sainte-Marie de Ré, LIAFA, CNRS et Université Denis Diderot, (consulté le )
- [Sakarovitch 2003] Jacques Sakarovitch, Éléments de théorie des automates, Vuibert, , 816 p. (ISBN 978-2-7117-4807-5)
- [Monmege et Schmitz 2011] Benjamin Monmege et Sylvain Schmitz, « Notes de révision : Automates et langages », Préparation à l’agrégation de mathématiques 2011–2012, LSV, ENS Cachan & CNRS, (consulté le ).
- [Schützenberger 1977] Marcel-Paul Schützenberger, « Sur une variante des fonctions séquentielles », Theoretical Computer Science, vol. 4, no 1, , p. 47-57 (ISSN 0304-3975, DOI 10.1016/0304-3975(77)90055-X, lire en ligne, consulté le ).
- [Eilenberg 1974] Samuel Eilenberg, Automata, Languages and Machines, Vol. A, Academic Press, coll. « Pure and Applied Mathematics » (no 58), , xvi+451 (ISBN 978-0-12-234001-7).
- [Ginsburg 1966] Seymour Ginsburg, The Mathematical Theory of Context-free Languages, New York, McGraw-Hill, .
- [Choffrut 1979] Christian Choffrut, « A generalization of Ginsburg and Rose's characterization of G-S-M mappings », dans ICALP 1979: Automata, Languages and Programming, Springer, coll. « Lecture Notes in Computer Science » (no 71), (ISSN 0302-9743, DOI 10.1007/3-540-09510-1_8), p. 88–103.
- [Ginsburg et Rose 1966] Seymour Ginsburg et Gene F. Rose, « A characterization of machine mappings », Can. J. Math., vol. 18, , p. 381–388 (MR 0191763).



























































