Attracteur d'Ikeda
L'attracteur d'Ikeda est un système dynamique à temps discret, caractérisé par la relation de récurrence :
- .

Attracteur d'Ikeda.
Il a été proposé en 1979 par le physicien japonais Kensuke Ikeda pour décrire la propagation de la lumière à travers une cavité optique non linéaire[1].
La relation de récurrence est souvent utilisée sous la forme[2] :
où est un paramètre et .
Lorsque , le système a un comportement chaotique.
Trajectoires
Les graphes ci-dessous représentent la trajectoire de 200 points, pour différentes valeurs du paramètre . Le graphe de gauche permet de visualiser l'attracteur et le point fixe, tandis que celui de droite est un zoom dans la région de l'attracteur et du point fixe.
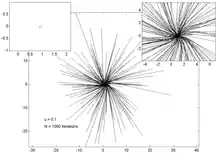 u = 0.1 |
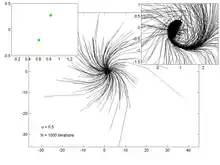 u = 0.5 |
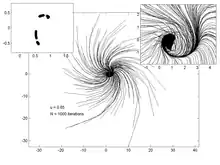 u = 0.65 |
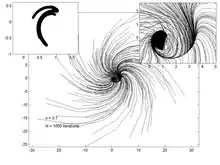 u = 0.7 |
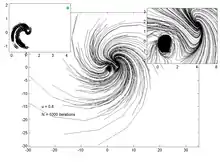 u = 0.8 |
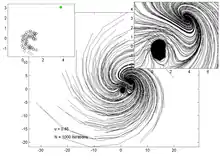 u = 0.85 |
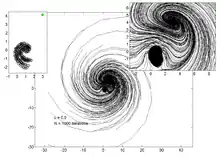 u = 0.9 |
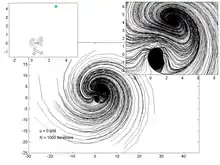 u = 0.908 |
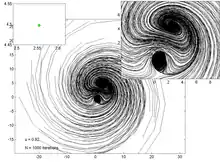 u = 0.92 |
Références
- (en) Kensuke Ikeda, « Multiple-valued stationary state and its instability of the transmitted light by a ring cavity system », Optics Communications (en), , p. 257-261 (lire en ligne)
- Meriem Halimi, Observation et détection de modes pour la synchronisation des systèmes chaotiques : une approche unifiée (Thèse de doctorat), , 112 p. (lire en ligne), p. 10-11
Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.





