Arbre splay

Pour insérer un nouveau nœud dans un arbre évasé :

• On commence par insérer ce nœud comme pour un arbre binaire de recherche.
• On évase ensuite l'arbre sur le nœud inséré afin de le placer à la racine.

Pour supprimer un nœud, on procède de façon similaire au cas d'un arbre binaire de recherche. Si le nœud a deux enfants, on échange la valeur de ce dernier avec son successeur direct dans ses sous-arbres et on cherche à supprimer le nœud dont on vient d'échanger la valeur. Dans tous les cas, on va ensuite évaser l'arbre sur le parent du nœud supprimé.

Pour réaliser un évasement sur le nœud ${\displaystyle X}$, on effectue une série d'étapes d'évasement, chacune rapprochant ${\displaystyle X}$ de la racine. Afin de déterminer quelle étape doit être réalisée, trois facteurs doivent être pris en compte :

• ${\displaystyle X}$ est-il l'enfant à droite ou à gauche de son parent ${\displaystyle P}$,
• ${\displaystyle P}$ est-il la racine,
• ${\displaystyle P}$ est il l'enfant à droite ou à gauche de son parent, le grand-parent ${\displaystyle G}$.

Après chaque étape, ${\displaystyle X}$ aura pris la place de ${\displaystyle G}$ (jusqu'à finir à la racine).

Deux opérations, zig et zag permettent alors de former toutes les combinaisons devant être réalisées : zig, zig-zig, zig-zag, zag, zag-zag et zag-zig. Les trois dernières étant les symétriques des trois premières nous nous concentrerons sur celles-là.

Une étape Zig sur un arbre évasé.

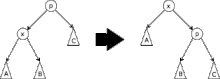
Dans le cas où ${\displaystyle P}$ est la racine, l'arbre est pivoté sur le lien entre ${\displaystyle X}$ et ${\displaystyle P}$. Cette étape n'existe que pour gérer les problèmes de parité et ne sera effectuée qu'en dernière opération (donc après une série de zig-zig et autres).

Une étape Zig-zig sur un arbre évasé dans le cas ou les deux nœuds X et P sont des enfants à gauche.

Lorsque ${\displaystyle X}$ et ${\displaystyle P}$ sont tous les deux enfants à droite (resp. gauche), l'arbre est alors pivoté deux fois : d'abord sur le lien entre ${\displaystyle P}$ et ${\displaystyle G}$, puis à nouveau sur le lien entre ${\displaystyle X}$ et ${\displaystyle P}$.

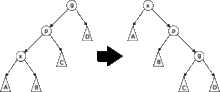
Une étape Zig-zag sur un arbre évasé, X étanbt initialement l'enfant à droite de P, lui même l'enfant à gauche de G.

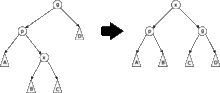
Lorsque ${\displaystyle X}$ et ${\displaystyle P}$ sont deux enfants différents (droite et gauche, ou vice-versa), on effectue d'abord une rotation sur le lien entre ${\displaystyle X}$ et ${\displaystyle P}$ puis une deuxième sur le lien entre ${\displaystyle P}$ et ${\displaystyle G}$.