Arbre de portée

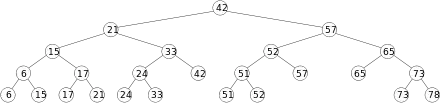
Un arbre de portée à 1 dimension d'un ensemble de n points est un arbre binaire de recherche, qui peut être construit en une complexité en temps de O(n log n)). Les arbres de portée de dimensions plus grande sont construites récursivement en construisant un arbre binaire de recherche équilibré sur la première coordonné des points, et ensuite, pour chaque sommet v dans cet arbre, en construisant un arbre de portée à (d-1) dimensions sur les points contenus dans le sous-arbre de v. Construire un arbre de portée de cette façon requiert un temps en O(nlog^dn)).

Cela peut être amélioré en remarquant qu'un arbre de portée sur un ensemble de points à 2 dimensions peut être construit en temps O(n log n)[7]. Soit S l'ensemble de n points à 2 dimensions. Si S contient seulement un point, retourner une feuille contenant ce point. Sinon, construire la structure associée de S, un arbre de portée de 1 dimensions sur la coordonnée y' des points dans S. Soit x_m la médiane des la coordonnée x des points. Soit 'S_L l'ensemble des points avec la coordonnée x inférieure ou égale à x_m et soit S_R l'ensemble des points avec la coordonnée x supérieure à x_m. Construire récursivement v_L, un arbre de portée à 2 dimensions sur S_L, et v_R, un arbre de portée à 2 dimensions sur S_R. Créer un sommet v avec pour enfant à gauche v_L et à droite v_R. Si on trie les points par leurs coordonnées y au début de l'algorithme, et en maintenant cet ordre quand on coupe les points par leurs coordonnées x, on peut construire la structure associée à chaque sous-arbre en temps linéaire. Cela réduit le temps pour construire un arbre de portée à 2 dimensions à O(n log n), ce qui réduit aussi le temps pour construire un arbre de portée à d dimensions à O(n log^d−1n).

Une requête de distance à 1 dimension [x₁, x₂]. Les points stockés dans les sous-arbres gris seront signalés. Trouver (x₁) et trouver (x₂) sera signalé s'ils sont à l'intérieur des bornes de la requête.

Les arbres de portée peuvent être utilisés pour trouver un ensemble de points qui se situent à un intervalle donné. Pour signaler les points dans l'intervalle [x₁, x₂], on commence par chercher x₁ et x₂. À certains sommets dans l'arbre, le chemin de recherche pour x₁ et x₂ va diverger. Soit v_split le dernier sommet que ces deux chemins de recherche ont en commun. On continue à chercher pour x₁ dans l'arbre de portée. Pour chaque sommet v dans le chemin de recherche depuis v_split à x₁, si la valeur stockée à v est plus grande que x₁, on signale chaque point dans le sous-arbre droit de v. Si v est une feuille, on signale la valeur stockée sur v si c'est à l'intérieur de l'intervalle de la requête. Similairement, on signale tous les points stockés dans le sous-arbre gauches avec les sommets qui ont une valeur inférieure à x₂ tout au long du chemin de recherche de v_split à x₂, et on signale la feuille de ce chemin si elle est à l'intérieur de l'intervalle de la requête.

Étant donné que l'arbre de portée est un arbre binaire équilibré, le chemin de recherche de x₁ et x₂ a une longueur de O(log n). Signaler tous les points stockés dans le sous-arbre d'un sommet peut être effectué en temps linéaire en utilisant un algorithme de parcours d'arbre. Ainsi le temps pour effectuer une requête de distance est O(log n + k), où k est le nombre de points dans l'intervalle de la requête.

Les requêtes de distance sont similaires dans d dimensions. Au lieu de signaler tous les points stockés dans les sous-arbres des chemins de recherche, on effectue une requête de distance à (d-1) dimensions sur la structure associée à chaque sous-arbre. Finalement, une requête de distance à 1 dimension va être effectuée et les points corrects vont être signalés.

De même, les requêtes de distance à 2 dimensions peuvent être effectuées. Un arbre binaire dans la coordonnée est nécessaire, où chaque nœud est augmenté avec un sous-arbre dans la coordonnée y qui contient tous les points descendants. Trivialement, cette structure de données peut être calculée en un temps de O(nlog²n) qui peut être optimisé en O(nlogn). Étant donné qu'on augmente chaque nœud avec un sous-arbre, la complexité de l'espace requis de cette structure de données est O(nlogn). La complexité en temps de chaque requête sera O(log²n).

Étant donné qu'une requête à d dimensions consiste en des requêtes de distance à O(log n) (d−1)dimensions , il survient que le temps pour effectuer une requête de distance à d dimensions est O(log^dn + k), où k est le nombre de points dans l'intervalle de la requête. Cela peut être réduit à O(log^d−1n + k) en utilisant la technique de cascade fractionnée[2] - [4] - [7].