Anneaux borroméens

La dénomination vient de l'utilisation qui en était faite dans les armoiries d'une famille italienne, les Borromeo. On retrouve néanmoins des anneaux borroméens bien avant cela, comme dans l'art bouddhique afghan du II^e siècle de l'ère chrétienne ou dans le symbole du Valknut en Scandinavie au VII^e siècle. On peut également en voir de rares représentations dans la mythologie grecque. Les anneaux borroméens ont été utilisés dans différents contextes pour symboliser la force et l'unité, notamment la religion et les arts.

Assimilés au triskèle, ils sont aussi parfois représentés comme emblème de l'unité des chevaliers de la table ronde dans les légendes arthuriennes.

• 
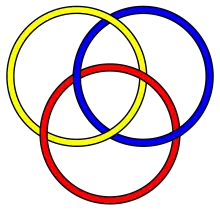  Nœud borroméen standard. Deux quelconques des cercles sont posés l'un sur l'autre sans se croiser et pourtant l'ensemble des trois cercles est lié par l'un d'entre eux.
• 
  Représenter un nœud borroméen en 3D implique une déformation de ses cercles.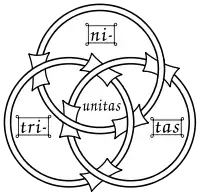
• 
  Anneaux borroméens utilisés comme symbole de la trinité chrétienne, image d'un manuscrit du XIII^e siècle

On retrouve aussi des nœuds borroméens partiels, dans lesquels trois éléments sont entrelacés de même manière que dans le nœud borroméen normal, mais où ces éléments ne sont pas fermés, comme le valknut servant de hache sacrificielle représenté sur la pierre de Snoldelev (en) ou l'emblème de Diane de Poitiers).

Anneaux borroméens en dimension 3, vus de face

Anneaux borroméens en dimension 3, vus de profil

Il n'est pas possible de réaliser matériellement des anneaux borroméens dans l'espace de dimension 3 à l'aide d'anneaux circulaires plats[1]. On peut donner l'illusion d'une telle réalisation en utilisant des anneaux courbés, donnant l'impression d'être circulaires lorsqu'ils sont vus sous un certain angle.

Nœud borroméen moléculaire

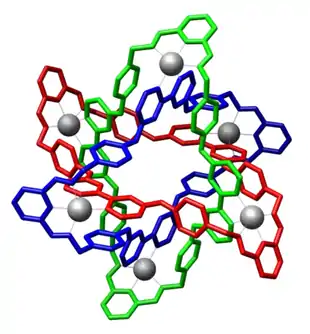
Les anneaux borroméens moléculaires (en) sont des architectures moléculaires mécaniquement entrelacées. C'est en 1997 que Chengde Mao et son laboratoire de l'université de New York réussissent à en construire avec de l'ADN circulaire[2].

Pour contextualiser l’utilisation du nœud borroméen dans la psychanalyse[3], soulignons tout d’abord que Jacques Lacan l’a découvert à 71 ans, auprès de quelqu’un qui fréquentait son séminaire et celui du mathématicien Georges-Théodule Guilbaud qui s’intéresse quant à lui à l’usage des mathématiques en sciences humaines. Lacan présente lui-même cette trouvaille de la manière suivante :

« Les nœuds c’est quelque chose d’assez original, avec peut-être — j’en suis sûr — l’ambiguïté de l’originel.  (…). Les trois ronds me sont donc venus comme bague au doigt, et j’ai tout de suite su que le nœud m’incitait à énoncer du symbolique, de l’imaginaire et du réel, quelque chose qui les homogénéisait[4]. »

C'est ainsi que Lacan choisit de représenter la structure du discours du sujet.

Dans son séminaire du 9 février 1972, Lacan crée une phrase à la structure borroméenne :

« Je te demande de me refuser ce que je t'offre parce que ce n'est pas ça[5] ! »

• Anneaux de Borromée sur MathCurve
• Contribution à l'étymologie du Noeud Borroméen en rapport avec notre sujet (Inconscient - Organisation sociale - Collectif, le 9 Mars 1990, Bernard Auriol, MD, psychanalyste et Pr Michel Benaim, PhD)