Angle de contact

Exemple d’angle de contact d’un liquide avec un substrat.

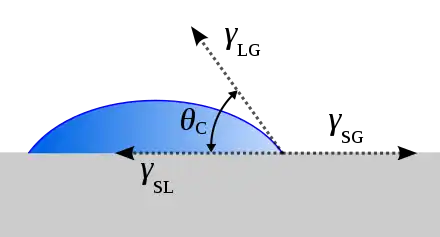
La description théorique de contact découle de l'examen (analyse) d'un équilibre thermodynamique entre les trois phases de la matière : la phase liquide de la goutte (L), la phase solide du substrat (S), et la phase gazeuse / vapeur de l’ambiant (G) (qui sera considéré comme un mélange de l'atmosphère ambiante et de la vapeur de liquide en équilibre avec sa phase liquide). La phase gazeuse pourrait également être une autre phase liquide (non miscible). À l'équilibre, le potentiel chimique de chacune des trois phases doit être identique. Il est plus convenable de recentrer ou d’analyser la discussion du point de vue d'énergies d’interface. Nous noterons l'énergie d’interface solide-vapeur (voir Énergie de surface) comme ${\displaystyle \gamma _{SG}}$, l'énergie d’interface solide-liquide comme ${\displaystyle \gamma _{SL}}$ et l'énergie liquide-vapeur (c'est-à-dire la Tension superficielle) simplement comme ${\displaystyle \gamma }$, nous pouvons donc écrire une équation qui doit être satisfaite à l'équilibre (connue sous le nom d'équation de Young) :

${\displaystyle 0=\gamma _{\mathrm {SG} }-\gamma _{\mathrm {SL} }-\gamma \cos \theta _{\mathrm {C} }\,}$

où ${\displaystyle \theta _{\mathrm {C} }}$ est l'angle de contact à l'équilibre. L'équation de Young suppose une surface parfaitement plane, et dans de nombreux cas la rugosité de surface et les impuretés provoquent à l'équilibre une déviation de l'angle de contact comparée à l'angle de contact prédit par l'équation de Young. Même dans une configuration de surface parfaitement lisse, une goutte de liquide adoptera une grande variété d'angles de contact compris entre l'angle de contact le plus grand (avançant), ${\displaystyle \theta _{\mathrm {A} }}$, et l'angle de contact le plus petit (reculant), ${\displaystyle \theta _{\mathrm {R} }}$. L'angle de contact à l'équilibre (${\displaystyle \theta _{\mathrm {C} }}$) peut être calculé à partir de ${\displaystyle \theta _{\mathrm {A} }}$ et ${\displaystyle \theta _{\mathrm {R} }}$ comme l'a démontré théoriquement Tadmor [1] avant d'être confirmé expérimentalement par Chibowski [2] :

${\displaystyle \theta _{\mathrm {C} }=\arccos {\frac {r_{\mathrm {A} }\cos {\theta _{\mathrm {A} }}+r_{\mathrm {R} }\cos {\theta _{\mathrm {R} }}}{r_{\mathrm {A} }+r_{\mathrm {R} }}}}$

où,

${\displaystyle r_{\mathrm {A} }={\sqrt[{3}]{\frac {\sin ^{3}{\theta _{\mathrm {A} }}}{2-3\cos {\theta _{\mathrm {A} }}+\cos ^{3}{\theta _{\mathrm {A} }}}}}}$

et,

${\displaystyle r_{\mathrm {R} }={\sqrt[{3}]{\frac {\sin ^{3}{\theta _{\mathrm {R} }}}{2-3\cos {\theta _{\mathrm {R} }}+\cos ^{3}{\theta _{\mathrm {R} }}}}}}$

L’angle de contact peut aussi être utilisé pour déterminer une énergie d’interface (si les autres énergies de surface sont connues). L’équation de Young peut être réécrite comme une autre équation connue sous le nom de l’équation Young-Dupré (Loi de Young-Dupré) :

${\displaystyle \gamma (1+\cos \theta _{\mathrm {C} })=\Delta W_{\mathrm {SLG} }\,}$

où ${\displaystyle \Delta W_{\mathrm {SLG} }}$ est l’énergie d’adhésion par unité de surface, entre la surface du substrat et celle du liquide, quand tous les deux sont dans le milieu G.

Une autre application de la mesure d'angle de contact est l'estimation de la qualité d'un mouillage : plus l'angle de contact entre un solide et un liquide est petit, plus le liquide mouille le solide, ce qui reflète une certaine affinité entre les deux éléments.

L'angle de contact diffère de sa valeur d'équilibre pour une interface qui avance ou qui recule, et ces deux valeurs dynamiques diffèrent aussi. On parle d'hystérésis d'angle de contact. L'angle dynamique est important dans un grand nombre de situations pratiques, c'est lui qui, par exemple, détermine la force extérieure qu'il faut exercer sur une goutte de liquide pour la faire glisser sur une surface solide. C'est seulement en 2017 qu'une modélisation thermodynamique des angles de contact dynamiques a pu être réalisée[3].

• Jacob Israelachvili, Intermolecular and Surface Forces, Academic Press (1985–2004)
• D.W. Van Krevelen, Properties of Polymers, 2nd revised edition, Elsevier Scientific Publishing Company, Amsterdam-Oxford-New York (1976)