Angle d'or

L'angle d'or est sous-tendu par l'arc b quand ${\displaystyle {\frac {a}{b}}=\varphi }$
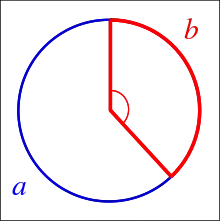
(φ étant le nombre d'or)..

En géométrie, l'angle d'or est l'angle sous-tendu par le plus petit des deux arcs créés en divisant la circonférence c d'un cercle en deux sections dont les longueurs a et b sont dans un rapport égal au nombre d'or φ.

En conséquence:

${\displaystyle c=a+b\,}$

${\displaystyle {\frac {a}{b}}={\frac {c}{a}}=\varphi ={\frac {1+{\sqrt {5}}}{2}}={\varphi }^{2}-1}$

L'angle d'or, sous-tendu par l'arc de cercle b, mesure en radians :

• ${\displaystyle \theta _{1}={\frac {2\pi }{\varphi ^{2}}}={2\pi }(1-{\frac {1}{\varphi }})=\pi (3-{\sqrt {5}})=2,39996323...}$

Comme l'arc intersecté par cet angle et la circonférence du cercle sont proportionnels :

• ${\displaystyle \theta _{1}/b={2\pi }/c}$
• ${\displaystyle \theta _{1}={2\pi }b/c}$
• ${\displaystyle \theta _{1}={2\pi }b/(a+b)}$
• ${\displaystyle \theta _{1}={2\pi }/(a/b+1)}$
• ${\displaystyle \theta _{1}={2\pi }/({\varphi }+1)={2\pi }{\frac {{\varphi }-1}{({\varphi }+1)({\varphi }-1)}}={2\pi }{\frac {{\varphi }-1}{({\varphi }^{2}-1)}}={2\pi }(1-1/{\varphi })={2\pi }(1-{\frac {2}{1+{\sqrt {5}}}})={2\pi }(1+{\frac {1-{\sqrt {5}}}{2}})=\pi (3-{\sqrt {5}})}$
• ${\displaystyle \theta _{1}={2\pi }/{\varphi }^{2}}$

Il mesure en degrés :

• ${\displaystyle {\frac {360}{\varphi ^{2}}}=180(3-{\sqrt {5}})=137,5077641...}$ soit 137° 30′ 27,950 5″

L'angle d'or rentrant, sous-tendu par l'arc de cercle a, mesure en radians :

• ${\displaystyle \theta _{2}=2\pi -\theta _{1}={\frac {2\pi }{\varphi }}=\pi ({\sqrt {5}}-1)=3,88322207...}$

Il mesure en degrés :

• ${\displaystyle {\frac {360}{\varphi }}=180({\sqrt {5}}-1)=222,492236...}$ soit 222° 29′ 32,049 4″

On retrouve cet angle à plusieurs reprises dans la nature[1]. Par exemple, les écailles des pommes de pin , ou les fleurons du tournesol[2] sont disposées le long de spirales logarithmiques, deux écailles ou fleurons successifs formant un angle d'or avec le centre de la spirale[3]. Apparaissent alors des spirales secondaires dont le nombre est toujours un élément de la suite de Fibonacci. Stéphane Durand explique que cette disposition correspond à l'optimisation de l'occupation de l'espace dans le plan[4]. Il existe des exposés détaillés de ce phénomène[5] - [6].

L’imagerie à résonance magnétique (IRM) utilise plusieurs méthodes d'échantillonnage. L'une d'elles, radiale avec incrémentation d'une valeur nommée « angle d'or », utilise la valeur 111,25°[7] - [8]

D'après la formule de Binet exprimant les nombres de Fibonacci : ${\displaystyle F_{n}={\frac {\varphi ^{n}-\psi ^{n}}{\sqrt {5}}}}$ où ${\displaystyle \psi =-1/\varphi }$, on a ${\displaystyle {F_{n} \over {\varphi }}-F_{n-1}\sim {\psi ^{n-1} \over {\sqrt {5}}}\longrightarrow 0}$ quand n tend vers l'infini.

On en déduit que ${\displaystyle F_{n}\theta _{2}-F_{n-1}.2\pi }$ tend vers 0 et que donc les multiples successifs de l'angle d'or rentrant par les nombres de Fibonacci tendent vers l'angle nul (et de même pour l'angle d'or (sortant)).