Algorithme des nœuds chapeaux

L'algorithme permet d'effectuer quatre opérations :

• déterminer si une quantité de ressource est disponible sur une période donnée du calendrier,
• réserver une quantité de ressource pour une période donnée,
• supprimer une réservation,
• décaler le calendrier (le calendrier couvrant une période de temps finie, il doit être régulièrement décalé au fur et à mesure que le temps passe).

L'intérêt de l'algorithme est que le temps d'exécution des 3 premières opérations dépend uniquement de la taille du calendrier (il est indépendant du nombre de réservations déjà effectuées).

La quantité de ressource à réserver est représentée par un nombre (par exemple un nombre de ko/s sur un lien de réseau).

Le calendrier est mémorisé sous forme d'un arbre binaire dans lequel une feuille représente une période élémentaire, et un nœud interne représente la période constituée par tous ses descendants.

Exemple d'un calendrier d'une durée de 7 heures (avec des périodes élémentaires d'une heure).

Pour une réservation donnée, on définit l'ensemble de ses "nœuds-chapeaux" qui est l'ensemble minimal de nœuds représentant la durée de la réservation.

Plus précisément, un nœud est un "nœud-chapeau" pour une réservation si et seulement si :

• toutes ses feuilles descendantes sont contenues dans la durée de la réservation,

et

• c'est le nœud racine, ou bien au moins une feuille descendante du nœud père est en dehors de la réservation.

Nœuds-chapeaux pour une réservation allant de 1h00 à 5h59.

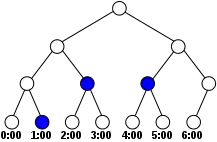
À chaque nœud est mémorisée la quantité de ressource réservée suivante :

q(nœud) = max (q(fils gauche), q(fils droit))
          + somme des quantités réservées pour les réservations ayant le nœud comme nœud-chapeau

(dans la pratique, pour des raisons d'optimisation, on mémorisera séparément les deux termes de cette somme).

L'enregistrement d'une réservation revient donc à ne mémoriser la quantité réservée que dans ses nœuds-chapeaux.

Soit "n" le nombre de périodes élémentaires du calendrier. On peut remarquer que le nombre de nœuds-chapeaux pour une réservation quelconque est inférieur ou égal à 2.log n, et que la détermination de ces nœuds-chapeaux se fait en O(log n).

• Détermination de la quantité de ressource disponible sur une période donnée : O(log n)
• Enregistrement d'une réservation : O(log n)
• Suppression d'une réservation : O(log n)
• Décalage du calendrier : O(log n + M.log n)

où M est le nombre de réservations actives pendant la période ajoutée en fin du calendrier.

M est nul si on s'interdit d'enregistrer des réservations au-delà de la durée du calendrier. Si M est important, on planifie en général le décalage du calendrier pendant les périodes creuses d'activité (souvent pendant la nuit).

On utilise la notation suivante :

q(nœud) = qf(nœud) + qn(nœud)
qf(nœud) = max (q(fils gauche), q(fils droit))
qn(nœud) = somme des quantités réservées pour les réservations ayant le nœud comme nœud-chapeau
t0(nœud) = début de la période représentée par le nœud
t1(nœud) = fin de la période représentée par le nœud
t0(resa) = début de la période de réservation
t1(resa) = fin de la période de réservation

qMax(nœud) = q(nœud) + somme des qn() des nœuds parents jusqu'à la racine de l'arbre

• Code source de l'algorithme, en langage C