Algorithme de Selfridge-Conway

Découpage de Selfridge et Conway.

Supposons l'existence de trois joueurs P1, P2 et P3. Lorsque la procédure donne un critère de décision, ce critère donne un choix optimal au joueur.

1. P1 divise le gâteau en trois morceaux qu'il considère de taille égale (selon sa mesure).
2. Appelons A le plus gros morceau selon la mesure de P2.
3. P2 coupe un peu de A pour le rendre de la même taille (selon la mesure de P2) que le deuxième plus grand morceau. A est alors divisé en : une part A1 et un résidu A2. On laisse le résidu A2 de côté pour le moment.
   • Si P2 pense que les deux plus grands morceaux sont maintenant égaux (de sorte qu'aucun ajustement supplémentaire n'est nécessaire), alors chaque joueur choisit une partie dans l'ordre P3, P2 et enfin P1.
4. P3 choisit un morceau entre A1 et les deux autres morceaux.
5. P2 choisit un morceau avec la limitation que si P3 n'a pas choisi A1, P2 doit le prendre.
6. P1 prend le dernier morceau en laissant juste le résidu A2 à diviser.

Il reste donc à diviser A2. Le morceau A1 a été choisi par P2 ou par P3 ; appelons le joueur qui l'a choisi PA et l'autre joueur PB.

1. PB découpe A2 en trois morceaux égaux.
2. PA choisit un morceau de A2 - noté A21.
3. P1 choisit un morceau de A2 - noté A22.
4. PB prend le dernier morceau de A2 - noté A23.

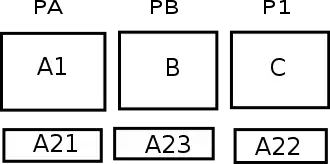
On peut alors montrer pourquoi cette procédure est sans jalousie. Pour cela, il faut démontrer que chaque joueur estime qu'aucun autre joueur n'a reçu plus que ce qu'il a lui-même reçu. Sans perte de généralité, on peut écrire (voir l'illustration ci-dessus):

• PA reçoit : A1 + A21.
• PB reçoit : B + A23.
• P1 reçoit : C + A22.

Dans l'analyse qui suit "plus grand" signifie "plus grand selon le joueur" :

• PA reçoit A1 + A21. Pour lui, A1 ≥ B et A1 ≥ C. Et il considère que son choix A21 est le plus grand morceau de A2. Ainsi, aucun autre joueur n'a reçu plus que ce lui : A1 + A21 ≥ B + A23, C + A22.
• PB reçoit B + A23. Pour lui, B ≥ A1 et B ≥ C puisqu'il a choisi B. De plus, c'est lui qui a découpé A2 en trois morceaux, tous  égaux selon lui. Donc B + A23 ≥ A1 + A21, C + A22.
• P1 reçoit C + A22. Pour lui, C ≥ A1 et C = B.
  • P1 estime que PB ne reçoit plus que lui. En effet, P1 a choisi son morceau de A2 avant de PB, donc A22 ≥ A23 selon lui. En d'autres termes : C + A22 ≥ B + A23.
  • P1 estime que PA ne reçoit pas non plus plus que lui. En effet, pour P1, C est égal à A puisqu'il a découpé le gâteau au premier tour. Comme A = A1 + A2 = A1 + (A21 + A22 + A23), C ≥ A1 + A21. (Ainsi, même si PA avait pris A2 en entier et que P1 n'avait pas reçu A22, P1 ne serait pas jaloux de PA.) En d'autres termes: C + A22 ≥ A1 + A21.

Si la seule contrainte est d'avoir une découpe sans jalousie pour une partie du gâteau, seule la première partie de l'algorithme de Selfridge-Conway  est nécessaire :

• P1 divise le gâteau en trois morceaux égaux pour lui ;
• P2 redécoupe au plus un morceau afin qu'il y ait deux morceaux de même taille pour lui ;
• P3 prend un morceau, puis P2, et enfin P1.

Cela garantit qu'il n'y a aucune jalousie et, en outre, chaque partenaire reçoit une valeur d'au moins 1/4 du total (puisque le nombre total de morceaux est de 4).

Cet algorithme peut être généralisé à 4 partenaires de la façon suivante[3] :

• P1 découpe le gâteau en 5 morceaux égaux pour lui ;
• P2 redécoupe au plus 2 morceaux, de manière qu'il existe alors 3 morceaux égaux pour lui ;
• P3 redécoupe au plus 1 morceau, de manière qu'il existe alors 2 morceaux de même taille pour lui ;
• P4 prend un morceau, puis P3, puis P2, et enfin P1.

Cela garantit qu'il n'y a pas de jalousie et, en outre, que chaque partenaire reçoit une valeur d'au moins 1/8 du total (puisque le nombre total de morceaux est de 8).

Par induction, la procédure peut être généralisée à n partenaires, le premier divisant le gâteau en ${\displaystyle 2^{n-2}+1}$ morceaux égaux et les partenaires continuent en les redécoupant. La division qui en découle est sans jalousie et chaque partenaire reçoit une valeur d'au moins ${\displaystyle 1/2^{n-1}}$ du total.

La même procédure peut être appliquée sur les restes. En faisant ainsi un nombre infini de fois, le gâteau tout entier est découpé sans jalousie[4]. Un raffinement de cet algorithme infini donne une variante finie de division sans jalousie : l'algorithme de Brams-Taylor (en).