Algorithme de Moore de minimisation d'un automate fini

L'algorithme de Moore opère par raffinement d'une partition des états de l’automate donné. L'algorithme maintient une partition des états, constituée initialement de deux classes, l'une formée des états terminaux et l'autre des autres états[3]. La partition est ensuite raffinée jusqu'à obtenir une partition stable. Le raffinement consiste à trouver des états séparables au sens suivant : deux états ${\displaystyle p}$ et ${\displaystyle q}$ sont séparables ou distinguables s'il existe un mot ${\displaystyle w}$ tel que l'état ${\displaystyle p\cdot w}$ est final et ${\displaystyle q\cdot w}$ n'est pas final, ou vice-versa. Dans le cas de l'algorithme de Moore, on remplace à chaque étape la partition courante par la partition qui est son intersection avec les partitions induites par les pré-images des classes par les lettres de l'alphabet.

Lorsque l'algorithme de raffinement s'arrête, chaque classe de la partition représente un ensemble d'états deux-à-deux inséparables, et deux classes distinctes sont séparables. L'automate minimal est obtenu en prenant comme états les classes de la partition, et comme transitions les transitions induites sur les classes par les transitions de l'automate de départ.

On considère un automate fini déterministe complet

${\displaystyle {\mathcal {A}}=(Q,i,T)}$

sur un alphabet ${\displaystyle A}$. Ici ${\displaystyle Q}$ est l'ensemble des états, ${\displaystyle i}$ est l'état initial, ${\displaystyle T}$ est l'ensemble des états terminaux. La fonction de transition est notée par un simple point. On suppose que tous les états sont accessibles[4].

L'algorithme est décrit par le pseudo-code suivant :

P := {T, Q \ T};                                           
répéter  
    P' := P                                              
    pour tout a de A faire
       calculer le raffinement de P induit par a; 
    remplacer P par son intersection avec ces raffinements        
jusqu'à P=P'

Plus formellement, on introduit une suite de relations d'équivalences sur l’ensemble des états notées ${\displaystyle \sim _{0},\sim _{1},\ldots }$ Ces équivalences sont définies par

${\displaystyle p\sim _{h}q\iff L_{q}^{(h)}({\mathcal {A}})=L_{p}^{(h)}({\mathcal {A}})}$,

où

${\displaystyle L_{p}^{(h)}({\mathcal {A}})=\{w\in A^{*}\mid p\cdot w\in T{\text{et }}|w|\leq h\}}$.

Les équivalences ${\displaystyle \sim _{h}}$ sont parfois appelées équivalences de Moore d'ordre ${\displaystyle h}$[5]. Chaque ensemble ${\displaystyle L_{p}^{(h)}}$ est composé des mots de longueur au plus ${\displaystyle h}$ qui mènent de l'état ${\displaystyle p}$ à un état terminal de l’automate. Deux états sont équivalents pour la relation ${\displaystyle \sim _{h}}$ si les mêmes mots de longueur au plus ${\displaystyle h}$ mènent à des états terminaux. Par exemple, la relation ${\displaystyle \sim _{0}}$ a deux classes, formées respectivement par les états terminaux et non terminaux. En fait, le langage ${\displaystyle L_{p}^{(0)}({\mathcal {A}})}$ est soit vide (si p n'est pas terminal), soit réduite au mot vide (si p est terminal). Plus généralement, dire que deux états sont dans la même classe d'équivalence de Moore d'ordre ${\displaystyle h}$ signifie que l'on ne peut pas séparer les deux états par des mots de longueur au plus ${\displaystyle h}$. Ce qui fait l’intérêt de ces équivalences est qu'ils se calculent facilement par récurrence grâce à la propriété suivante : Pour deux états ${\displaystyle p}$ et ${\displaystyle q}$ et ${\displaystyle h\geq 0}$, on a

${\displaystyle p\sim _{h+1}q\iff p\sim _{h}q\quad }$ et ${\displaystyle \quad p\cdot a\sim _{h}q\cdot a}$ pour toute lettre ${\displaystyle a\in A}$.

Ainsi, pour calculer l'équivalence ${\displaystyle \sim _{h+1}}$, on détermine les états qui, par une lettre, arrivent dans des classes distinctes de ${\displaystyle \sim _{h}}$ : ceux-ci sont dans des classes distinctes de ${\displaystyle \sim _{h+1}}$. Pratiquement on prend les lettres de l’alphabet l'une après l'autre ; pour une lettre ${\displaystyle a\in A}$, on calcule la partition dont les classes sont constituées d'états qui, par la lettre ${\displaystyle a}$, donnent des états équivalents pour ${\displaystyle \sim _{h}}$. On forme ensuite l'intersection de ces partitions avec la partition ${\displaystyle \sim _{h}}$ elle-même.

Il est facile de vérifier que si ${\displaystyle \sim _{k}}$ et ${\displaystyle \sim _{k+1}}$ sont égales pour un entier ${\displaystyle k}$, alors ${\displaystyle \sim _{k}}$ et ${\displaystyle \sim _{k+r}}$ sont égales pour tout ${\displaystyle r}$, et que les classes d'équivalences sont formées d'états inséparables.

Automate minimal équivalent à l'automate du haut de la page. Les états sont les classes de l'équivalence de Moore d'ordre 2.

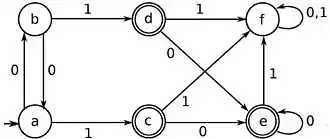
L'exemple donné au début de la page est un automate à six états, sur l’alphabet {0,1}. Il n'est pas difficile de calculer directement les six langages ${\displaystyle L_{p}=\{w\in A^{*}\mid p\cdot w\in T\}}$ : On a

${\displaystyle L_{a}=L_{b}=0^{*}10^{*},L_{c}=L_{d}=L_{e}=0^{*}L_{f}=\emptyset }$

et les états se répartissent en trois classes d'états indistinguables, donnant la partition (a,b|c,d,e|f). On peut aussi facilement calculer les langages ${\displaystyle L_{p}^{(h)}}$ : On a

${\displaystyle L_{a}^{(0)}=L_{b}^{(0)}=L_{f}^{(0)}=\emptyset ,L_{c}^{(0)}=L_{d}^{(0)}=L_{e}^{(0)}=\varepsilon }$,

${\displaystyle L_{a}^{(1)}=L_{b}^{(1)}=1,L_{f}^{(1)}=\emptyset ,L_{c}^{(1)}=L_{d}^{(1)}=L_{e}^{(1)}=\{\varepsilon ,0\}}$,

${\displaystyle L_{a}^{(2)}=L_{b}^{(2)}=\{1,01\},L_{f}^{(2)}=\emptyset ,L_{c}^{(2)}=L_{d}^{(2)}=L_{e}^{(2)}=\{\varepsilon ,0,00\}}$.

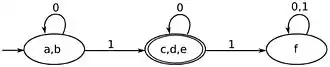
La partition de départ, définie par l'équivalence ${\displaystyle \sim _{0}}$, est composée des classes ${\displaystyle \{a,b,f\}}$ et ${\displaystyle \{c,d,e\}}$, notée ${\displaystyle (a,b,f|c,d,e)}$. La partition induite par les images, par la lettre 1, est la partition ${\displaystyle (a,b|c,d,e,f)}$. De même, les états dont l'image, par la lettre 0, est un état final, sont ${\displaystyle c,d,e}$, la partition est ${\displaystyle (a,b,f|c,d,e)}$. L'intersection de ces deux partitions est la partition ${\displaystyle (a,b|c,d,e|f)}$. L'intersection avec la partition ${\displaystyle (a,b,f|c,d,e)}$ de ${\displaystyle \sim _{0}}$ donne ${\displaystyle (a,b|c,d,e|f)}$, qui est la partition de ${\displaystyle \sim _{1}}$. Pour calculer la partition ${\displaystyle \sim _{2}}$ suivante, on calcule la partition des images par 0 et aussi par 1, des classes de ${\displaystyle \sim _{1}}$. Ce sont des classes déjà entièrement contenues dans ces classes ; on a donc ${\displaystyle \sim _{1}=\sim _{2}}$. Ceci confirme le calcul ci-dessus des ${\displaystyle L^{(1)}}$ et ${\displaystyle L^{(2)}}$. L'automate minimal a donc ces trois états ; il est donné dans la figure ci-contre.

Un automate à minimiser.

On considère l’automate ci-contre à 8 états numérotés de 0 à 7, et sur un alphabet à deux lettres a et b. La table de transition est formée des deux premières colonnes du tableau ci-dessous. L'état initial est 0, les états 0,3,4,6,7 sont terminaux. L'équivalence ${\displaystyle \sim _{0}}$ est composée de deux classes, celle des états terminaux et celle des états non terminaux. On note A={0,3,4,6,7} et B={1,2,5} ces deux classes. Sur le tableau, elles sont représentées par une colonne supplémentaire.

	a	b	${\displaystyle \sim _{0}}$	a	b	${\displaystyle \sim _{1}}$	a	b
0	2	1	A	B	B	X	Z	Y
1	2	1	B	B	B	Y	Z	Y
2	3	2	B	A	B	Z	T	Z
3	5	4	A	B	A	T	Z	T
4	5	4	A	B	A	T	Z	T
5	6	5	B	A	B	Z	T	Z
6	5	7	A	B	A	T	Z	T
7	5	7	A	B	A	T	Z	T

Les colonnes suivantes sont indicées par a et b. Pour chaque ligne ${\displaystyle q}$ et chaque colonne ${\displaystyle a}$, l'entrée contient la classe à laquelle appartient l'état ${\displaystyle q\cdot a}$. On obtient deux colonnes supplémentaires. Sur chaque ligne, le triplet de classes correspond à une intersection de classes de la partition de ${\displaystyle \sim _{1}}$ qui est l'intersection de la partition de ${\displaystyle \sim _{0}}$ avec les images inverses de ses classes par les lettres. Il y a quatre triplets : (A,B,B), (B,B,B) (B,A,B) et (A,B,A). L'équivalence ${\displaystyle \sim _{1}}$ a donc les quatre classes ${\displaystyle (0|1|25|3467)}$. On les note X, Y, Z, T. On répète l'opération, avec les nouvelles classes. On constate alors que les nouveaux triplets sont encore au nombre de quatre : (X,Z,Y), (Y,Z,Y), (Z,T,Z) et (T,Z,T). L'équivalence ${\displaystyle \sim _{2}}$ a donc les quatre même classes. L'automate minimal a donc quatre états, et les trois dernières colonnes et les quatre premières lignes de la table donnent la table de sa fonction de transition.

La complexité en temps de l'algorithme est, dans le pire des cas, ${\displaystyle O(sn^{2})}$, où ${\displaystyle s}$ est la taille de l'alphabet et où ${\displaystyle n}$ est le nombre d'états de l'automate. Chacune des étapes du raffinement peut être effectuée en temps ${\displaystyle O(sn)}$ en utilisant une variante appropriée du tri par base ou « radix sort ». À chaque étape, le nombre de classes augmente strictement, et comme au départ il y a deux classes, au plus ${\displaystyle n-2}$ étapes suffisent. En fait, la complexité est même en ${\displaystyle O(\ell sn)}$, où ${\displaystyle \ell }$ est le nombre d'étapes de l'algorithme. On peut observer[5] que le nombre d'étapes est indépendant du nombre d'états de l'automate de départ. En effet, chaque état d'un automate reconnaissant un langage ${\displaystyle L}$ correspond à un résiduel ${\displaystyle u^{-1}L}$ pour un mot ${\displaystyle u}$. L'algorithme consiste donc à identifier ces langages - les mêmes pour chaque automate - en calculant leurs mots par longueur croissante.

La complexité en moyenne est bien meilleure. Elle est en ${\displaystyle O(n\log n)}$, et même en ${\displaystyle O(n\log \log n)}$, selon le choix du modèle retenu pour la distribution aléatoire[5] - [6].

• Algorithme de Brzozowski de minimisation d'un automate fini
• Algorithme de Hopcroft de minimisation d'un automate fini

Article de Moore

• Edward F. Moore, « Gedanken-experiments on sequential machines », dans Automata studies, Princeton, N. J., Princeton University Press, coll. « Annals of mathematics studies » (n^o 34), 1956 (MR 0078059), p. 129–153.

Manuels

• Olivier Carton, Langages formels, calculabilité et complexité, 2008 [détail de l’édition] (lire en ligne)
• (en) John E. Hopcroft, Rajeev Motwani et Jeffrey D. Ullman, Introduction to Automata Theory, Languages, and Computation, Addison-Wesley, 2007, 3^e éd. (ISBN 978-0-32146225-1)
• Jacques Sakarovitch, Éléments de théorie des automates, Paris, Vuibert, 2003, 816 p. (ISBN 978-2-7117-4807-5, zbMATH 1188.68177)
• Patrice Séébold, Théorie des automates : méthodes et exercices corrigés, Vuibert, 1999, 198 p. (ISBN 978-2-7117-8630-5)

Article de synthèse

• Jean Berstel, Luc Boasson, Olivier Carton et Isabelle Fagnot, « Minimization of Automata », dans Automata: from Mathematics to Applications, European Mathematical Society, 2010 (arXiv 1010.5318)

Article

• (en) Norbert Blum, « An O(n log n) implementation of the standard method for minimizing n-state finite automata », Information Processing Letters, vol. 57, n^o 2,‎ 1996, p. 65–69 (DOI 10.1016/0020-0190(95)00199-9).