Algorithme de Las Vegas
En informatique, un algorithme de Las Vegas est un type d'algorithme probabiliste qui donne toujours un résultat correct ; son caractère aléatoire lui donne de meilleures performances temporelles en moyenne[2]. Comme le suggère David Harel dans son livre d'algorithmique[3], ainsi que Motvani et Raghavan[2], le tri rapide randomisé[4] est un exemple paradigmatique d'algorithme de Las Vegas.
| Découvreur ou inventeur | |
|---|---|
| Date de découverte |
1979[1] |
| Problème lié |
Algorithmic paradigm (en) |
| À l'origine de |
| Pire cas | |
|---|---|
| Meilleur cas |
Quand le problème que l'algorithme résout possède plusieurs solutions, sur une même donnée, comme c'est le cas pour le tri d'un tableau qui contient des clés équivalentes, l'algorithme de Las Vegas peut retourner l'une ou l'autre de ces solutions, et il le fait de façon non prévisible.
Exemple du tri rapide randomisé
Dans cette section, nous expliquons l'exemple du tri rapide randomisé qui est un algorithme de Las Vegas.
Description de l'algorithme
L'algorithme de tri rapide aléatoire, ou quicksort randomisé consiste à trier un tableau d'éléments en utilisant diviser pour régner :
- choisir aléatoirement un pivot (i.e. un élément du tableau) ;
- partitionner le tableau en plaçant les éléments strictement plus petits que le pivot à gauche (sous-tableau A), puis le pivot, puis les éléments plus grands que le pivot (sous-tableau B) ;
- trier récursivement les sous-tableaux A et B.
Le résultat est un tableau constitué d'un tri du tableau A, suivi du pivot, suivi d'un tri du tableau B.
Analyse du temps d'exécution


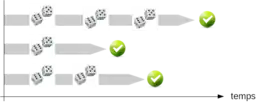
L'aléatoire se situe au niveau du choix des pivots. Le résultat est un tableau trié, quels que soient les choix de pivots, i.e. le résultat est toujours correct. En revanche, le temps d'exécution dépend de ces choix. C'est, en fait, un tri souvent utilisé sur des tableaux de grandes tailles parce que, de manière empirique, il donne de bons résultats en complexité temporelle[5]. Dans les figures à droite, l'algorithme est exécuté deux fois sur le même échantillon ; on voit que l'on obtient un tableau trié dans les deux cas, alors que les pivots sont choisis aléatoirement.
- Si l'algorithme choisit toujours le pivot le plus petit (ou le plus grand)[6], alors le partitionnement est déséquilibré. Le temps d'exécution vérifie l'équation de récurrence et on a .
- Si l'algorithme pouvait choisir toujours le pivot médian, c'est-à-dire au milieu du tableau (par une sorte d'oracle), la relation de récurrence serait et on a .
Pour simuler l'oracle, on prend un choix aléatoire du pivot en espérant qu'il nous donnera souvent un pivot situé pas très loin de la médiane.
Proposition d’implémentation
La version Las Vegas du tri rapide choisit aléatoirement le pivot dans la liste à trier, tout en gardant le reste de l'algorithme inchangé. En voici le code en langage Python :
# Import des modules nécessaires
from random import * # Outils et fonctions d'aléatoires
# Fonction de séparation de listes selon le pivot
def separation(liste, pivot, n):
"""
Entrée: une liste, un pivot et la place du pivot dans la liste
Sortie: deux listes
- la première contenant les éléments plus petits que le pivot
- la seconde contenant les éléments plus grands ou égal au pivot
"""
# Les listes à remplir
listePetit = []
listeGrand = []
# Traitement liste à séparer
for (i, x) in enumerate(liste):
# Exclusion du pivot
if i == n: continue
# Séparation
if x >= pivot: listeGrand.append(x)
else: listePetit.append(x)
# for
# On renvoie le tuple contenant les deux listes
return (listePetit, listeGrand)
# separation()
# Fonction tri rapide
def quicksort(liste):
"""
Entrée: une liste
Sortie: la liste triée
"""
# Longueur de la liste
n = len(liste)
# Une liste vide ou à un élément est toujours triée
if n <= 1: return liste
# Choix du pivot au hasard dans la liste
i = randint(0, n - 1)
pivot = liste[i]
# Séparation de la liste en deux sur le pivot
(petit, grand) = separation(liste, pivot, i)
# Appel récursif sur chacune des listes et regroupement des résultats
return quicksort(petit) + [pivot] + quicksort(grand)
# quicksort()
Existence d'une stratégie optimale pour les algorithmes de Las Vegas
Étant donné un algorithme de Las Vegas A, Luby, Sinclair et Zuckerman ont étudié comment minimiser l'espérance du temps requis pour obtenir la réponse de A. Pour cela ils adoptent une stratégie[7] qui indique, quand relancer l'algorithme[8]. On note TA(x) le temps d'une exécution de A sur l'entrée x ; ce temps n'est pas toujours le même, c'est une variable aléatoire.
Etant donné A et une entrée x, les stratégies, telles que Luby et al. les considèrent, ont la forme suivante :
- On se fixe une entier t1 et on effectue t1 étapes de l'algorithme A sur l'entrée x. S'il s'est arrêté, alors la stratégie se termine.
- Sinon, on se fixe un autre entier t2 et on effectue t2 étapes de l'algorithme A sur l'entrée x. S'il s'est arrêté, alors la stratégie se termine.
- Sinon, etc.
Ainsi, une stratégie S a une deuxième composante, à savoir une suite infinie d'entiers, de sorte que nous pouvons écrire une stratégie sous la forme S(A, t1, t2, ...). Une stratégie est optimale si elle minimise l'espérance du temps de son exécution sur x pour un A fixé. Luby et al. donne une stratégie optimale de la forme S(A, t*, t*, ...) où t* dépend de la distribution de probabilité de TA(x). Le calcul de t* demande à connaître cette distribution. On note l'espérance du temps d'exécution de la stratégie optimale.
Cependant, en général, on ne connaît pas la distribution de probabilité de TA(x). C'est pourquoi Luby et al. montre l'existence d'une stratégie dite universelle dont l'espérance du temps d'exécution n'est pas trop éloignée de l'espérance de la stratégie optimale, à savoir que son espérance est . Cette stratégie est S(A, 1, 1, 2, 1, 1, 2, 4, 1, 1, 2, 1, 1, 2, 4, 8, 1, ...) et ne requiert, comme on le voit, aucune connaissance sur la distribution de TA(x).
Définition et comparaison avec les algorithmes de Monte Carlo et d'Atlantic City
Algorithme de Las Vegas
Un algorithme de Las Vegas est un algorithme probabiliste (utilisant le hasard) qui fournit toujours un résultat juste. Ainsi, l'algorithme renverra toujours une solution au problème posé mais sa complexité temporelle n'est pas prévisible. Par des bons choix lors des points clés de l'exécution de l'algorithme, on doit pouvoir montrer que cette complexité est faible.
Ces algorithmes ont été ainsi nommés par Laszlo Babai en 1979 par métonymie avec les algorithmes de Monte-Carlo. On nommera par la suite une troisième famille d'algorithmes probabilistes les algorithmes d'Atlantic City, en référence aux nombreux jeux d'argent se déroulant dans ces trois villes.
Algorithmes de Monte-Carlo
Les algorithmes de Monte-Carlo sont des algorithmes probabilistes qui utilisent le hasard pour renvoyer la meilleure réponse possible en un temps fixé. La complexité temporelle est donc fixé pour ces algorithmes. Cependant, la justesse du résultat est soumise à une incertitude.
Algorithmes d'Atlantic City
Les algorithmes d'Atlantic City essayent de tirer le meilleur des deux méthodes précédentes. Ce type d'algorithme renverra presque toujours un résultat juste en un temps presque toujours fixé. L'incertitude se situe donc sur la complexité temporelle et sur la justesse du résultat.
Conclusion
Exprimé autrement :
- un algorithme de Las Vegas s'arrête quand il a trouvé une réponse exacte ;
- un algorithme de Monte-Carlo répond dans un temps prévisible et court sans pour autant garantir une réponse exacte (voir tests de primalité probabilistes) ;
- un algorithme d'Atlantic City est relativement rapide et donne une réponse exacte avec une bonne garantie de l'exactitude.
Notes et références
- Algorithms and Theory of Computation Handbook, CRC Press LLC, 1999, "Las Vegas algorithm", in Dictionary of Algorithms and Data Structures [online], Paul E. Black, ed., U.S. National Institute of Standards and Technology. 17 July 2006. (accessed May 09, 2009) Available from:
- (en) Rajeev Motwani et Prabhakar Raghavan, Randomized Algorithms, Cambridge, New York et Melbourne, Cambridge University Press, (réimpr. 1997, 2000), 1re éd., 476 p. (ISBN 978-0-521-47465-8, lire en ligne), chap. 1.2 (« Introduction: Las Vegas and Monte Carlo »), p. 9-10
- https://brilliant.org/wiki/randomized-algorithms-overview/
- (en) Laszlo Babai, Monte-Carlo algorithms in graph isomorphism testing (Technical Report), Université de Montréal, Canada, (lire en ligne).
- (en) Rajeev Motwani et Prabhakar Raghavan, Randomized Algorithms, Cambridge University Press, , 476 p. (ISBN 978-0-521-47465-8, lire en ligne), section 1.2, p. 9
- (en) David Harel, Computers Ltd : What They Really Can't Do, Oxford University Press, (lire en ligne), p. 130
- (en) Robert Sedgewick, « Implementing Quicksort Programs », Commun. ACM, vol. 21, no 10, , p. 847-857 (DOI 10.1145/359619.359631)
- (en) S. Dasgupta, C.H. Papadimitriou, U.V. Vazirani, Algorithms, , 318 p., p. 62; The Unix Sort Command
- (en) Thomas H. Cormen, Charles E. Leiserson et Ronald L. Rivest, Introduction à l'algorithmique : cours et exercices, Paris, Dunod, , xxix+1146 (ISBN 978-2-10-003922-7, SUDOC 068254024), chap. 7 (« Tri rapide »)
- Une « stratégie » est une succession de choix d'exécution, qui prend un algorithme (ici l'algorithme A), comme l'une de ses composantes.
- (en) Michael Luby, Alistair Sinclair et David Zuckerman, « Optimal speedup of Las Vegas algorithms », Information Processing Letters Volume 47, Issue 4, , Pages 173-180 (lire en ligne)







