Algorithme d'Ukkonen

L'algorithme d'Ukkonen lit les caractères les l'un après l'autre, en faisant grossir la structure qu'il produit, de telle sorte que, à tout instant, l'arbre obtenu est l'arbre des suffixes du préfixe lu. Cette lecture des caractères du mot, qui progresse de gauche à droite, confère à l'algorithme d'Ukkonen son incrémentalité. Dans le premier algorithme de construction de l’arbre des suffixes, proposé par Peter Weiner, celui-ci lit le mot du dernier caractère au premier, produisant les arbres des suffixes, du plus petit suffixe du mot donné au plus grand suffixe du mot (c'est-à-dire le mot lui-même)[2]. Edward M. McCreight propose plus tard un algorithme plus simple, allant toujours de droite à gauche dans la lecture du mot[3]. Dans sa présentation, Esko Ukkonen propose d'abord sa version quadratique incrémentale de gauche à droite qu'il linéarise ensuite.

L'implémentation naïve de la construction d'un arbre de suffixes en lisant le mot du début à la fin requiert une complexité temporelle O (n²) voire O(n³) en notation de Landau, où n est la longueur de la chaîne. En exploitant un certain nombre de techniques algorithmiques, l'algorithme d'Ukkonen réduit ce temps à O(n) (linéaire), pour les alphabets de taille constante, et O(n log n) en général, correspondant aux performances d'exécution des deux précédents algorithmes.

Explicitons l'exécution sur le mot ${\displaystyle baobab}$. L'algorithme part de l'arbre ne contenant qu'une racine. Lisons les lettres de ${\displaystyle baobab}$ de gauche à droite.

Étape 1 : insertion de ${\displaystyle b}$ dans l'arbre.

Comme aucune arête partant de la racine n'est étiquetée par ${\displaystyle b}$, on construit un nœud correspondant au suffixe ${\displaystyle b}$. À ce stade, on a construit un arbre suffixe correspondant au mot ${\displaystyle b}$ dont le seul suffixe est ${\displaystyle b}$.

Étape 2 : insertion de ${\displaystyle a}$ dans l'arbre.

À ce stade, le mot entier considéré est ${\displaystyle ba}$. Le suffixe ${\displaystyle b}$ devient ${\displaystyle ba}$ et on ajoute le suffixe ${\displaystyle a}$ dans l'arbre.

À ce stade, le mot entier considéré est ${\displaystyle ba}$. Le suffixe ${\displaystyle b}$ devient ${\displaystyle ba}$ et on ajoute le suffixe ${\displaystyle a}$ dans l'arbre.

Étape 3 : insertion de ${\displaystyle o}$ dans l'arbre.

À ce stade, le mot entier considéré est ${\displaystyle bao}$. Comme précédemment, on met à jour les suffixes ${\displaystyle ba}$ et ${\displaystyle a}$ qui deviennent respectivement ${\displaystyle bao}$ et ${\displaystyle ao}$ puis on ajoute ${\displaystyle o}$ comme suffixe.

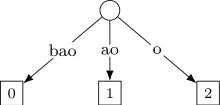
Étape 4 : insertion de ${\displaystyle b}$ dans l'arbre.

À ce stade, le mot entier considéré est ${\displaystyle baob}$. On met à jour les suffixes ${\displaystyle bao}$, ${\displaystyle ao}$ et ${\displaystyle o}$ qui deviennent respectivement ${\displaystyle baob}$, ${\displaystyle aob}$ et ${\displaystyle ob}$. En revanche, il n'est pas nécessaire d'insérer le suffixe ${\displaystyle b}$ qui est déjà présent dans l'arbre via l'arête ${\displaystyle baob}$. (on retient maintenant que les prochaines modifications vont avoir lieu sur l'arête ${\displaystyle baob}$, et que le plus long préfixe commun est ${\displaystyle b}$. On garde ces informations).

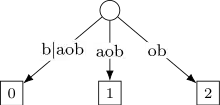
Étape 5 : insertion de ${\displaystyle a}$ (mot considéré est ${\displaystyle baoba}$) :

L'arête courante est ${\displaystyle baob}$, dont ${\displaystyle ba}$ est toujours le préfixe. Il suffit donc de mettre à jour les suffixes ${\displaystyle baob}$, ${\displaystyle aob}$ et ${\displaystyle ob}$ qui deviennent ${\displaystyle baoba}$, ${\displaystyle aoba}$ et ${\displaystyle oba}$. Le plus long préfixe commun devient ${\displaystyle ba}$.

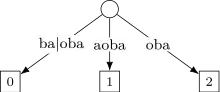
Étape 6 insertion de ${\displaystyle b}$ (mot considéré est ${\displaystyle baobab}$) :

Les suffixes ${\displaystyle baoba}$, ${\displaystyle aoba}$ et ${\displaystyle oba}$ deviennent ${\displaystyle baobab}$, ${\displaystyle aobab}$ et ${\displaystyle obab}$. En revanche, le suffixe ${\displaystyle bab}$ n'est plus préfixe de ${\displaystyle baobab}$. Il faut scinder l'arête ${\displaystyle baobab}$ après ${\displaystyle ba}$ qui est le plus long préfixe commun.

• Étape 6.1 : on insère un nœud entre ${\displaystyle ba}$ et ${\displaystyle obab}$, puis on rajoute une arête ${\displaystyle b}$ partant de ce nœud (on a introduit un branchement). On a ainsi ajouté les suffixes ${\displaystyle baobab}$ et ${\displaystyle bab}$ dans l'arbre. Il reste à traiter les suffixes ${\displaystyle ab}$ et ${\displaystyle b}$.
  
• Étape 6.2 : le suffixe ${\displaystyle ab}$ a comme plus long préfixe commun ${\displaystyle a}$ avec l'arête ${\displaystyle aobab}$. On sépare donc l'arête ${\displaystyle aobab}$ en insérant un nœud entre ${\displaystyle a}$ et ${\displaystyle obab}$. On ajoute également une arête ${\displaystyle b}$ partant de ce nœud
  
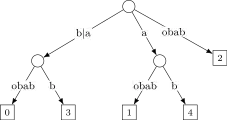
• Étape 6.3 : le suffixe ${\displaystyle b}$ a comme plus long préfixe ${\displaystyle b}$ avec l'arête ${\displaystyle ba}$. On insère donc encore un nœud entre ${\displaystyle b}$ et ${\displaystyle a}$ sur l'arête ${\displaystyle ba}$

• Arbre des suffixes
• Algorithme en ligne

• Explication détaillée en anglais
• Recherche rapide de chaînes avec des arbres de suffixes Tutoriel de Mark Nelson. Présente un exemple d'implémentation écrit en C++.
• Implémentation en C avec explication détaillée
• Diapositives de la conférence de Guy Blelloch
• Page d'accueil d'Ukkonen
• Projet d'indexation de texte (construction en temps linéaire d'Ukkonen d'arbres de suffixes)
• Implémentation en C Partie 1 Partie 2 Partie 3 Partie 4 Partie 5 Partie 6