AC0
En théorie de la complexité, AC0 est une classe de complexité définie par des circuits booléens de profondeur constante. Elle fait partie de la hiérarchie AC. La classe AC0 contient l'addition, mais pas la fonction parité, la multiplication ou le prédicat de primalité (voir plus bas).
Définition
La classe AC0 est la classe de complexité des problèmes décidés par des circuits booléens de profondeur constante, de taille polynomiale, dont les portes sont des ET et des OU, de degrés entrants non bornés[1] - [2] (en fait, d'autres portes peuvent être autorisés comme des portes "OU exclusif" ou NON car elles sont exprimables, sans changer la complexité, par des ET et des OU). Le sigle AC vient de alternation circuit[2]. Elle fait partie de la hiérarchie AC.
Exemples
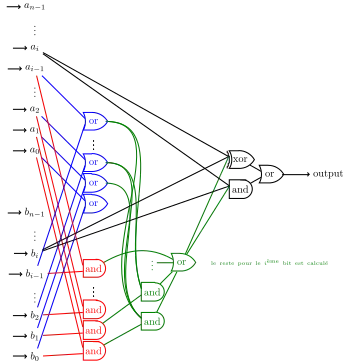
L'addition est dans AC0. Plus précisément, pour tout i, le problème de décision qui prend en entrée 2n bits qui représente deux nombres a et b de n bits et qui calcule le ième bit de la somme de a et b est dans AC0.
Voici une façon de construire[3] un circuit pour calculer le ième bit de la somme de an-1...a0 et bn-1...b0. Notons ∧ le "et" logique, ∨ le "ou" logique et ⊕ le ou exclusif. On considère aj comme une proposition, vraie si le jème bit de a vaut 1, et fausse sinon. De même, bj comme une proposition, vraie si le jème bit de b vaut 1, et fausse sinon. De même, on note sj comme une proposition, vraie si le jème bit de s vaut 1, et fausse sinon. On introduit également d'autres propositions :
- rj est vraie s'il y a une retenue pour le jème bit, fausse sinon ;
- gj est vraie si une retenue est générée au jème bit, fausse sinon ;
- pj est vraie si la retenue éventuelle est propagée au jème bit, fausse sinon.
On a :
- gj = aj ∧ bj
- pj = aj ∨ bj
- rj = (g0 ∧ p1 ∧ ... ∧ pj-1) ∨ (g1 ∧ p2 ∧ ... ∧ pj-1) ∨ ... ∨ gj-1
- sj = (aj ⊕ bj ⊕ rj) ∨ (aj ∧ bj ∧ rj) si j ≤ n
- sn+1 = rn+1
Le nombre de portes du circuit correspondant aux formules ci-dessus est polynômial en n. Aussi, la profondeur du circuit est constante comme le montre le circuit présenté en illustration ci-dessus.
De même la soustraction est dans AC0.
Exemples de problèmes hors AC0
Parité
La fonction parité est un prédicat qui renvoie 1 si dans l'entrée le nombre de bits 1 est pair, et qui renvoie 0 sinon. Dans les années 1970, on ne savait pas s'il existait des circuits AC0 pour le problème de la clique ou le problème du voyageur de commerce[1]. En fait, Furst, Saxe et Sipser[4], et indépendamment Miklós Ajtai[5] ont démontré que ce n'est pas le cas. Ils ont même démontré qu'un prédicat beaucoup plus simple, à savoir la fonction parité, n'appartient pas à AC0. Johan Håstad a ensuite montré un résultat plus fort[1], le switching lemma (en)[6]. Comme la fonction parité est dans NC1, on en déduit que l'inclusion de AC0 dans NC1 est stricte.
Majorité
La fonction majorité prend en entrée n bits et retourne 1 si strictement plus de la moitié des bits valent 1. Cette fonction n'est pas dans AC0. On peut démontrer cela par l'absurde[7], si majorité est dans AC0, en ajoutant des bits supplémentaires, on peut tester si x ≥ k, où x est l'entier représenté par les bits en question et k est une constante ; à partir de là on peut tester si x = k ; et donc tester la parité, tout en étant dans AC0, ce qui est une contradiction.
Multiplication
La multiplication n'est pas dans AC0 et on le montre par réduction depuis la fonction parité[8]. En revanche, elle est dans NC1.
Complexité descriptive
La classe AC0 est liée à la logique du premier ordre en complexité descriptive[10].
Notes et références
- (en) Sanjeev Arora et Boaz Barak, Computational Complexity : A Modern Approach, Cambridge University Press, (ISBN 0-521-42426-7), chap. 14 (« Circuit lower bounds »), p. 248
- Sylvain Perifel, Complexité algorithmique, Ellipses, , 432 p. (ISBN 9782729886929, lire en ligne), chap. 5 (« Uniformité et non-uniformité »)
- (en) « Cours de Kristoffer Arnsfelt Hansen sur AC », sur Site de Kristoffer Arnsfelt Hansen à l'université Aarhus (Dannemark), p. 2
- Merrick Furst, James B. Saxe et Michael Sipser, « Parity, circuits, and the polynomial-time hierarchy », Math. Syst. Theory, vol. 17, , p. 13-27 (ISSN 0025-5661, DOI 10.1007/bf01744431, zbMATH 0534.94008)
- Miklós Ajtai, « ∑ 1 1-formulae on finite structures », Annals of pure and applied logic, vol. 24, no 1, , p. 1-48
- Johan Håstad, « Almost Optimal Lower Bounds for Small Depth Circuits », dans Proceedings of the 18th Annual {ACM} Symposium on Theory of Computing, May 28-30, 1986, Berkeley, California, {USA}, (DOI 10.1145/12130.12132), p. 6-20
- (en) « Lecture 3: AC0, the switching lemma »
- (en) « Lecture 5 on AC0 and TC0 »
- Eric Allender, Michael Saks et Igor Shparlinski, « A Lower Bound for Primality », Journal of Computer and System Sciences, vol. 62, , p. 356–366 (DOI 10.1006/jcss.2000.1725, lire en ligne, consulté le )
- (en) Neil Immerman, Descriptive Complexity, New York, Springer-Verlag, , 268 p. (ISBN 0-387-98600-6, présentation en ligne).