Équilibre du navire
L'équilibre du navire correspond au comportement d'un navire dans l'eau. Ce dernier subit un certain nombre de forces comme son poids, la poussée d’Archimède, etc. Son comportement est étudié afin de sécuriser la navigation. Un dossier complet établi par le chantier naval ou l'architecte naval doit recevoir le visa d'une société de classification reconnue puis être soumis à l'autorité compétente [1].
Équilibre statique
Pour expliquer l'équilibre d'un navire sur l'eau à l'arrêt[2], il est nécessaire de définir trois notions importantes : le centre de gravité, le centre de carène et le métacentre de carène.
Le centre de gravité « G » est le lieu d'application du poids du navire. On préfère s'arranger pour qu'il ne se déplace pas vers le coté où penche déjà le navire, ce qui amplifierait le phénomène. On arrime donc la cargaison pour qu'elle reste fixe. Il est également prudent de descendre le centre de gravité le plus bas possible : c'est le rôle du lest.
La carène étant la partie immergée de la coque d'un navire, le centre de carène est le centre géométrique du volume immergé (volume du fluide déplacé), et donc le lieu d'application de la poussée d'Archimède, verticale vers le haut. Le centre de carène est noté « C » (pour carène) ou « B » (pour buoyancy, flottabilité en anglais).
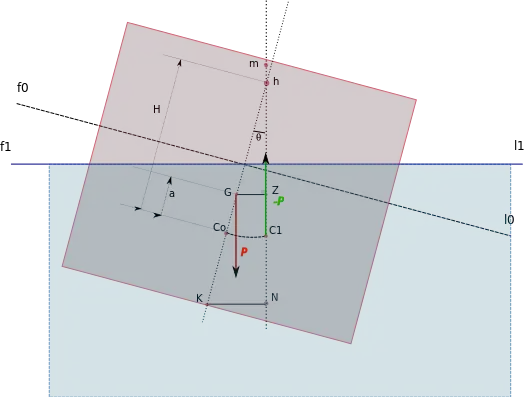
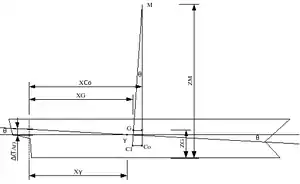
La position du centre de carène varie avec les tirants d'eau (l'enfoncement), l'assiette et la gîte (sur le schéma on a représenté deux positions, Co en C1) ; cependant, en première approximation et pour les variations suffisamment petites de position du centre de carène, il existe un point où se croisent toutes les poussées d'Archimède correspondant à ces différentes positions : c'est le métacentre de carène, m sur le schéma.
Il est facile de comprendre qu'un navire dont le centre de gravité est en-dessous du centre de carène reste stable : il est comme un pendule simple, où le centre de carène joue le rôle de point d'accroche du pendule et le centre de gravité celui de la masse. Cependant cette condition n'est pas nécessaire, et n'est pas réalisée pour, par exemple, une simple planche homogène moins dense que l'eau : le centre de gravité, correspondant au milieu dela planche, est manifestement plus haut que le centre de carène, qui lui est au milieu de la partie immergée. Et pourtant la planche reste stable. Si le centre de gravité est plus haut que le centre de carène (à l'exemple impressionnant d'un porte-conteneurs), le modèle pertinent n'est pas le pendule, mais plutôt le culbuto ou la chaise à bascule : lorsque le navire penche, pour qu'il revienne à sa position de départ il suffit que le centre de carène se déplace plus fortement encore dans un sens adéquat. Ce qui compte c'est donc le métacentre.
L'équilibre du navire est conditionné par les positions respectives de ces deux points : le centre de gravité et le métacentre. De celles-ci découleront la gîte, l'assiette et la stabilité initiale.
Les conditions nécessaires pour que le navire soit stable sont :
- le déplacement (son poids) du navire doit être égal à la poussée d'Archimède (autrement dit, le navire doit flotter[3]) ;
- le centre de gravité doit se trouver au-dessous du métacentre de carène : dans ce cas, lorsqu'une perturbation déplace le centre de gravité ou le centre de carène, et que les deux forces (poids et poussée d'Archimède) ne sont plus sur la même verticale, elles forment un couple qui va faire tendre à les remettre sur la même verticale et à restaurer cette situation qui est celle d'équilibre parfait.
Lorsque le navire s'incline, le centre de carène se déplace de Co en C1,(on considère que pour de petites inclinaisons, le centre de carène décrit une portion d'arc de cercle de centre m le métacentre de carène. On peut l'assimiler à un centre de rotation instantané relatif à une inclinaison donnée. On nomme le point h point métacentrique. On notera que h est à une distance infinie lorsque l'inclinaison est nulle.)
Le rayon de ce cercle peut être calculé par la formule de Bouguer :
est le moment quadratique de la surface de flottaison par rapport à son axe d'inclinaison (exprimé en m⁴) et le volume de carène (exprimé en m³).
Il se forme un couple de redressement de moment tendant à faire retrouver au navire sa position initiale droite. P est le poids et GZ le bras de levier.
On peut remarquer que plus G sera haut et se rapprochera de m, plus le bras de levier de redressement GZ sera faible. Lorsque GZ sera nul il n'existera pas de bras de levier de redressement, le navire continuera à s'incliner, ou du moins sera en équilibre instable. Lorsque G est au-dessus de m, le bras de levier sera inclinant et augmentera l'inclinaison, jusqu'à atteindre une position d'équilibre qui peut être à 180° (à l'envers).
Le phénomène simple le plus approchant est l'équilibre d'une chaise à bascule. Le métacentre a une position fixée, ici elle est le centre du cercle dont la base de la chaise à bascule forme des arcs de ce cercle. La position du centre de gravité de l'ensemble (homme + chaise) est variable selon la position que prend l'homme. Une personne assise entraîne une stabilité de la chaise (centre de gravité au-dessous du métacentre), si la personne se met debout sur la chaise, le centre de gravité de l'ensemble monte au-dessus du métacentre et la position devient instable. La dernière image montre une très forte stabilité, la chaise est vide, le centre de gravité est très bas.
 Personne debout--Position instable (G au-dessus de M)
Personne debout--Position instable (G au-dessus de M) Personne assise--Position stable (G en dessous de M)
Personne assise--Position stable (G en dessous de M) Position droite stable
Position droite stable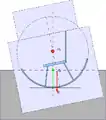 Position très stable (G est très bas)
Position très stable (G est très bas)
La position du centre de gravité du navire (G) doit être surveillée. Un chargement dans les hauts fera monter G, un chargement dans les bas fera descendre G. Un navire commencera donc, de manière générale, par charger dans les fonds avant de charger dans les compartiments supérieurs. La valeur de GM est sujette à des réglementations (SOLAS), entre autres: un minimum de l'ordre de 0,30 m voire 0,45 m pour certains navires.
Dans le triangle GZH rectangle en Z: , et aussi
Le moment du couple de redressement peut donc s'écrire:.
Module de stabilité initial transversal
Le module de stabilité initial transversal est défini par ou r représente le h pris dans le domaine de la stabilité transversale uniquement.
r se remplace en utilisant le théorème de Bouguer :
P se remplace par sa valeur en fonction du volume de carène V et de la masse volumique de l'eau
Ce module peut être séparé en deux membres :
Ici, intervient le moment de la surface de flottaison qui dépend de la forme de la carène, et la masse volumique de l'eau. Le marin n'a aucune emprise sur ce terme, c'était l'affaire de l'architecte naval à la création du navire qui a cherché à obtenir une stabilité de forme positive, jusqu'à un angle de gite déterminé.
Dans ce second terme, le déplacement P est trouvé mais aussi « a ». Par convention « a » est compté positivement lorsque G est au-dessus de C. Il s'agit donc de la position du centre de gravité G mesurée à partir du centre de carène C. Le membre est négatif. Le marin peut influencer ce dernier, en modifiant la position du centre de gravité du navire, soit par ajout ou suppression de poids, soit par déplacement de poids. Il s'agit de la stabilité de poids qui peut être positive ou négative.
Dans le cas d'un voilier monocoque le moment de redressement peut rester positif jusqu'au renversement presque complet grâce à la présence d'une quille lestée abaissant fortement le centre de gravité
La courbe de stabilité statique
La courbe de stabilité statique, aussi communément appelée courbe en "GZ", est une représentation graphique de la stabilité statique transversale d'un navire.
Quant au terme GZ, il représente le bras de levier redressant et est déterminé par la disposition horizontale de « G » (Centre de gravité du navire) et « B » (Centre de carène du navire) pour chaque angle d'inclinaison.
Lors d'un chavirement, le bras de levier redressant "GZ" augmentera jusqu'à atteindre un maximum puis se mettra à diminuer ou, atteignant un certain angle d'inclinaison, il deviendra négatif et donc un bras de levier chavirant.
En calculant les valeurs de "GZ" pour certains angles d'inclinaison d'un navire ayant un chargement bien défini permettra de produire la courbe de stabilité statique pour cette situation. Il en suit que plus grandes seront les valeurs de "GZ", plus grande sera l'aire sous la courbe. Laquelle est sujette à des standards minimum spécifiés dans le "Code on Intact Stability"[4] incorporé dans la législation gouvernementale de la plupart des pays qui ont signé les conventions de l'Organisation maritime internationale[5].
Procédure pour construire une courbe de stabilité statique (courbe GZ)
- Déterminer le déplacement du navire et son "KG" effectif pour ces conditions ("KG" effectif prend en compte les effets de surfaces libres dans les compartiments).
- Dans les données hydrostatiques, trouver la valeur de la hauteur initiale du métacentre ("KM") pour ce même déplacement du navire.
- Déterminer la hauteur de "GM" corrigée, utilisant la formule :
- Rechercher les valeurs de "KN" pour tous les angles d'inclinaison donnés dans les tables "KN" (ou courbes "KN"). Et même si les valeurs de "KN" de changent pas exactement linéairement, l'interpolation des valeurs intermédiaires de "KN" permettra d'obtenir une courbe "GZ" plus précise.
- Déterminer les valeurs de "GZ" pour les angles d'inclinaison donnés, utilisant la formule
- Tracer point par point les valeurs de "GZ".
- Avant de joindre tous les points de la courbe, tracer une verticale à un angle de 57.3° (=1 radian). Tracer la valeur effective de "GM", sur l'échelle de "GZ", et tracer une horizontale passant ce point en direction de la droite. Pour finir, tracer une droite de l'origine jusqu'à l'intersection de ces deux droites. Celle-ci indiquera la tangente initiale à la courbe aux petits angles d'inclinaison, ce qui permet d'assister le tracé initial de la courbe de stabilité statique ("GZ").
- "GZ" et "GM" sont très proches aux petits angles d'inclinaison ()
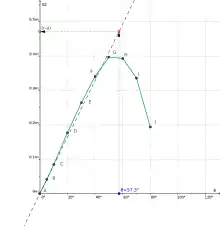 Exemple de tracé
Exemple de tracé
Informations pouvant être extraites de la courbe de stabilité statique
L'analyse de cette courbe peut révéler de précieuses informations assez rapidement et ainsi aider les officiers de marine marchande, pour lesquels la stabilité de leurs navires est une priorité.
- Les valeurs de GZ pour tous angles d'inclinaison possible. Ces valeurs pourront ainsi être utilisées pour calculer le moment de stabilité statique du navire à cet angle d'inclinaison choisi, en utilisant la formule suivante :
- La valeur maximale de "GZ" et l'angle d'inclinaison auquel elle apparaît.
- L'étendue sur laquelle une stabilité positive est présente, ainsi que l'angle de stabilité neutre.
- Une approximation de l'angle auquel le livet de pont commence à être immergé ().
Cet angle peut être intensifié sur la courbe comme étant le point d'inflexion de celle-ci (point où la courbe passe d'une augmentation concave vers une forme convexe). Celui-ci est souvent assez difficile à estimer précisément. Mais tracer des verticales à intervalles réguliers peut aider à définir la variation de l'inclinaison de la courbe, en considérant l'orientation des droites entre deux points d'intersection de deux verticales consécutives.
Module de stabilité initial longitudinal
On définira le module de stabilité initial longitudinal où R représente le h pris dans le domaine de la stabilité longitudinale uniquement.
Comme le précédent, ce module peut être séparé en deux membres, donnant stabilité de forme et stabilité de poids, mais le membre stabilité de forme est tellement grand car R dans le domaine longitudinal est de l'ordre de la longueur du navire, que la stabilité de poids est négligeable.
Notes et références
- https://www.legifrance.gouv.fr/codes/section_lc/JORFTEXT000000841523/LEGISCTA000021113104/ Division 211
- Lorsque le navire se déplace, il faut en plus considérer les forces de poussée par le moteur ou la voilure, et la résistance de l'eau, voire de l'air, sur la coque. Pour un navire à moteur, la poussée qu'il produit est dans l'axe et ne contribue pas à la gite, alors que c'est le cas sur un voilier : l'effort sur une voile, n'est pas uniquement vers l'avant mais également vers le coté du navire.
- Si la poussée d'archimède excède le déplacement, le navire remonte et la poussée d'Archimède se réduit. Si c'est l'inverse, le navire s'enfonce et la poussée d'Archimède s'accroit, soit suffisamment pour rétablir l'équilibre, soit non et le navire coule.
- /http://www.imo.org/en/OurWork/Safety/StabilityAndSubdivision/Pages/Default.aspx
- /http://www.imo.org/EN/Pages/Default.aspx
Voir aussi
Bibliographie
- E. Guyou, Des variations de stabilité des navires, dans Revue maritime et coloniale, tome 79, octobre-, p. 532-545 (lire en ligne)
- Kai Krieger et Marc Fouliard, Les cahiers maritimes, calculs de stabilité : livre 1 et cédérom, version 1.1, Infomer, (ISBN 2-913596-29-0 et 978-2-913596-29-0, OCLC 492991750, lire en ligne).
Articles connexes
Liens externes
- Feuille interactive de calcul
- [Basic ship theory by K.J.Rawson]
- Gm-meter
- [PDF]Stabilité du navire (Dominique Lavoille)



















