Tonneau (formules)

Pour trouver la capacité d'un tonneau, ou jaugeage, beaucoup de formules ont été proposées. Celles-ci sont en général approchées, une formule exacte nécessitant de connaître la forme précise du tonneau.

Quelques formules historiques

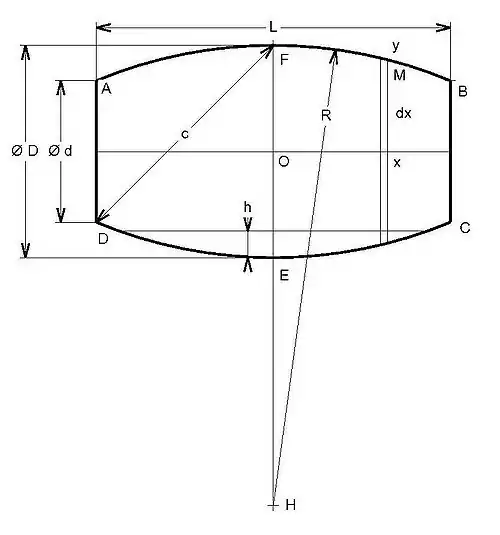
Tonneau couché

On se donne la hauteur L du tonneau, le diamètre minimal d, dit diamètre du fond, et le diamètre maximal D, dit diamètre du bouge. La plupart des formules historiques reviennent à approximer le volume du tonneau par celui d'un cylindre de même hauteur, mais de diamètre intermédiaire entre celui du fond et celui du bouge.

Kepler a donné une formule approchée

V={\frac {\pi L}{12}}(D^{2}+Dd+d^{2})

Ce volume est celui de deux troncs de cône réunis par leur base de diamètre D. Il sous-estime légèrement le volume du tonneau.

Oughtred a modifié la formule :

V={\frac {\pi L}{12}}(2D^{2}+d^{2})

Cette formule correspond précisément à un tonneau dont le profil est celui d'un arc d'ellipse.

Une instruction du ministère de l'Intérieur en pluviôse de l'an VII fixa la formule suivante[1] :

V={\frac {\pi L}{4}}\left(D-{\frac {1}{3}}(D-d)\right)^{2}={\frac {\pi L}{4}}\left(d+{\frac {2}{3}}(D-d)\right)^{2}

Ou encore :

V={\frac {\pi L}{36}}(2D+d)^{2}

Dez[2] a établi la formule :

V={\frac {\pi L}{4}}\left(d+{\frac {5}{8}}(D-d)\right)^{2}

Ou encore : $V={\frac {\pi L}{256}}(5D+3d)^{2}$

Les Douanes emploient la formule :

V=0{,}625\;C^{3}

Dans laquelle $C$ représente la diagonale allant du trou de bonde au point le plus éloigné de ce trou. Elle est très rapide, car elle n'exige qu'une seule mesure.

Calcul

La forme générale des tonneaux consiste en une surface de révolution engendrée par une portion de courbe et terminée par deux plans parallèles équidistants de l'équateur. Le volume se calcule de la façon suivante :

V=\int S\,\mathrm {d} x

Où $S$ est la surface du disque de rayon $y$

V=2\pi \int _{0}^{\frac {L}{2}}y^{2}\,\mathrm {d} x

Les formes les plus usuelles sont données par les exemples qui suivent.

Parabole

On choisit l'axe du tonneau comme axe de la parabole. L'équation de la parabole est de la forme $y=ax^{2}+b$ , avec $a={\frac {2(d-D)}{L^{2}}}$ et $b={\frac {D}{2}}$ . Le polynôme s'intègre facilement, et on obtient :

V={\frac {\pi L}{60}}(8D^{2}+3d^{2}+4Dd)

Ellipse

Elle a pour équation ${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1$ , où $a={\frac {L}{2{\sqrt {1-\left({\frac {d}{D}}\right)^{2}}}}}$ et $b={\frac {D}{2}}$ . D'où la formule $V=2\pi b^{2}\int _{0}^{\frac {L}{2}}\left(1-{\frac {x^{2}}{a^{2}}}\right)\mathrm {d} x$ qui s'intègre facilement elle aussi, et on obtient :

V={\frac {\pi L}{12}}(2D^{2}+d^{2})

On retrouve la formule d'Oughtred.

Cercle

C'est la courbe qui vient immédiatement à l'esprit, car elle est facile à tracer au compas. L'équation s'exprime par : $x^{2}+(y-b)^{2}=R^{2}$ (cercle de centre H, de rayon R et passant par A et B), avec $b={\frac {D^{2}-d^{2}-L^{2}}{4(D-d)}}$ et $R={\frac {(D-d)^{2}+L^{2}}{4(D-d)}}$ . D'où $V=2\pi \int _{0}^{\frac {L}{2}}(b+{\sqrt {R^{2}-x^{2}}})^{2}\mathrm {d} x$ et finalement :

V=\pi \left(L\left(b^{2}+R^{2}-{\frac {L^{2}}{12}}\right)+2bR^{2}\left(\arcsin {\frac {L}{2R}}+{\frac {L}{2R}}{\sqrt {1-\left({\frac {L}{2R}}\right)^{2}}}\right)\right)

Noter que si l'on réalise un développement limité à l'ordre 2 de cette formule suivant $\varepsilon ={\frac {D-d}{L}}$ , on retrouve la formule de la parabole donnée plus haut.

Cosinus

On prend $y=a\cos(bx)$ avec $a={\frac {D}{2}}$ et $b={\frac {2}{L}}\arccos {\frac {d}{D}}$ , ce qui donne $V=2\pi \int _{0}^{\frac {L}{2}}{\frac {D^{2}}{4}}\cos ^{2}(bx)\mathrm {d} x$ et :

V={\frac {\pi D^{2}L}{8}}\left(1+{\frac {{\frac {d}{D}}{\sqrt {1-\left({\frac {d}{D}}\right)^{2}}}}{\arccos {\frac {d}{D}}}}\right)

Comparaison des formules

Application numérique d'un cas réel. Les cotes sont en décimètres pour des résultats directs en litres.

d = 6,06 dm (petit diamètre)

D = 7,01 dm (diamètre du bouge)

L = 8,05 dm (longueur)

c = 7,68 dm (cas de la formule des Douanes)

b = -13,79 dm (cas du cercle), pour mémoire, car b dépend de d, D et L

R = 17,29 dm (cas du cercle), pour mémoire, car R dépend de d, D et L

Formule	Volume (litres)
Kepler (troncs de cônes)	270,48
Oughtred (ellipse)	284,52
Dez	279,91
Douanes	283,12
Pluviôse an VII	283,25
Parabole	283,76
Cercle	283,90
Cosinus	283,51

Volume d'un tonneau de section elliptique

Soient A et B les diamètres de la section elliptique du bouge, et soient a et b les diamètres des fonds.

Si on a des paraboles comme génératrices, on a les formules :

Dans le plan xOy :

$y={\frac {2(a-A)}{L^{2}}}x^{2}+{\frac {A}{2}}$

Dans le plan xOz :

$z={\frac {2(b-B)}{L^{2}}}x^{2}+{\frac {B}{2}}$

$V=2\int _{0}^{\frac {L}{2}}\pi yz\mathrm {d} x$

$V={\frac {\pi L}{60}}(3ab+2aB+2Ab+8AB)$

Volume partiel en fonction de la hauteur de liquide

La génératrice est la parabole d'équation : $y={\frac {2(d-D)}{L^{2}}}x^{2}+{\frac {D}{2}}$

Pour un tonneau couché

Soit $h$ la hauteur de liquide

Soit $x_{1}$ et $x_{2}$ les bornes maximales selon les valeurs de $h$

$x_{1}={\sqrt {\frac {hL^{2}}{2(D-d)}}}$ et $x_{2}={\sqrt {\frac {(D-h)L^{2}}{2(D-d)}}}$

$V=\int S\mathrm {d} x$

Où $S$ représente le segment circulaire, de rayon $y$ , de flèche $y-{\frac {D}{2}}+h$ .

$S=y^{2}\left(\arccos {\frac {D-2h}{2y}}-{\frac {D-2h}{2y}}{\sqrt {1-\left({\frac {D-2h}{2y}}\right)^{2}}}\right)$

Si $h\leq {\frac {D-d}{2}}$ , alors

$V=\int _{0}^{x_{1}}2S\mathrm {d} x$

Si ${\frac {D-d}{2}}\leq h\leq {\frac {D+d}{2}}$ , alors

$V=\int _{0}^{\frac {L}{2}}2S\mathrm {d} x$

Si $h\geq {\frac {D+d}{2}}$ , alors

$V=\int _{0}^{x_{2}}2S\mathrm {d} x+\int _{x_{2}}^{\frac {L}{2}}2\pi y^{2}\mathrm {d} x$

Pour un tonneau debout

$V=\int _{{\frac {L}{2}}-h}^{\frac {L}{2}}\pi y^{2}\mathrm {d} x$

${\begin{aligned}V&=\pi {\Biggl [}{\frac {4(d-D)^{2}}{5L^{4}}}\left(\left({\frac {L}{2}}\right)^{5}-\left({\frac {L}{2}}-h\right)^{5}\right)\\\ &+{\frac {2D(d-D)}{3L^{2}}}\left(\left({\frac {L}{2}}\right)^{3}-\left({\frac {L}{2}}-h\right)^{3}\right)+h\left({\frac {D}{2}}\right)^{2}{\Biggr ]}\end{aligned}}$

Surfaces

On considère ici aussi la parabole comme génératrice. Soit $S_{1}$ cette surface

$S_{1}=2\int _{0}^{\frac {L}{2}}2\pi y\mathrm {d} s$

où $\mathrm {d} s$ est la différentielle de l'abscisse curviligne.

$\mathrm {d} s={\sqrt {1+y'^{2}}}\mathrm {d} x$

$S_{1}=4\pi \int _{0}^{\frac {L}{2}}(ax^{2}+b){\sqrt {1+4a^{2}x^{2}}}\mathrm {d} x$

L'intégration se fait par le changement de variable : $2ax=\sinh t$

On arrive à :

${\begin{aligned}S_{1}&={\frac {\pi L}{4}}{\Biggl [}{\sqrt {{\frac {4(d-D)^{2}}{L^{2}}}+1}}\left(d+D+{\frac {L^{2}}{8(d-D)}}\right)\\\ &+{\frac {L}{d-D}}\left(D-{\frac {L^{2}}{16(d-D)}}\right)\operatorname {argsinh} {\frac {2(d-D)}{L}}{\Biggr ]}\end{aligned}}$

Puis on ajoute les deux fonds : $S_{2}={\frac {\pi d^{2}}{2}}$

$S=S_{1}+S_{2}$

Surface du tonneau en contact avec le liquide

Tonneau couché

Si $h\leq {\frac {D-d}{2}}$ , alors

$S=\int _{0}^{x_{1}}4y\arccos {\frac {D-2h}{2y}}{\sqrt {1+4a^{2}x^{2}}}\ \mathrm {d} x$

Si ${\frac {D-d}{2}}\leq h\leq {\frac {D+d}{2}}$ , alors

${\begin{aligned}S&=\int _{0}^{\frac {L}{2}}4y\arccos {\frac {D-2h}{2y}}{\sqrt {1+4a^{2}x^{2}}}\ \mathrm {d} x\\\ &+{\frac {1}{2}}\left(d^{2}\left(\arccos {\frac {D-2h}{d}}-(D-2h){\sqrt {d^{2}-(D-2h)^{2}}}\right)\right)\end{aligned}}$

Si $h\geq {\frac {D+d}{2}}$ , alors

${\begin{aligned}S&=\int _{0}^{x_{2}}4y\arccos {\frac {D-2h}{2y}}{\sqrt {1+4a^{2}x^{2}}}\ \mathrm {d} x\\\ &+\int _{x_{2}}^{\frac {L}{2}}4\pi \left(ax^{2}+{\frac {D}{2}}\right){\sqrt {1+4a^{2}x^{2}}}\ \mathrm {d} x+{\frac {\pi d^{2}}{2}}\end{aligned}}$

Tonneau debout

$0<h<L$ et en tenant compte d'un fond :

$S=2\pi \int _{{\frac {L}{2}}-h}^{\frac {L}{2}}\left(ax^{2}+{\frac {D}{2}}\right){\sqrt {1+4a^{2}x^{2}}}\ \mathrm {d} x+\pi {\frac {d^{2}}{4}}$

Si $h=0$ alors $S=0$ . Et si $h=L$ le tonneau est plein. Voir supra.

${\begin{aligned}S&={\frac {\pi L}{8}}{\Biggl [}{\sqrt {1+{\frac {4(d-D)^{2}}{L^{2}}}}}\left(d+D+{\frac {L^{2}}{8(d-D)}}\right)\\\ &-{\frac {L-2h}{L}}{\sqrt {1+{\frac {4(d-D)^{2}(L-2h)^{2}}{L^{4}}}}}\left({\frac {(d-D)(L-2h)^{2}}{L^{2}}}+{\frac {L^{2}}{8(d-D)}}+2D\right)\\\ &+{\frac {L}{d-D}}\left(D-{\frac {L^{2}}{16(d-D)}}\right)\left(\operatorname {argsinh} {\frac {2(d-D)}{L^{2}}}-\operatorname {argsinh} {\frac {2(d-D)(L-2h)}{L^{2}}}\right){\Bigg ]}\\\ &+{\frac {\pi d^{2}}{4}}\end{aligned}}$

Surface de liquide en contact avec l'air

Tonneau couché

La génératrice est la parabole.

La corde $c$ au point d'abscisse $x$ s'exprime par :

$c={\sqrt {4y^{2}-(D-2h)^{2}}}$

Si $h\leq {\frac {D-d}{2}}$ ,

$S=\int _{0}^{x_{1}}2c\ \mathrm {d} x$

Si ${\frac {D-d}{2}}\leq h\leq {\frac {D+d}{2}}$ , alors

$S=\int _{0}^{\frac {L}{2}}2c\ \mathrm {d} x$

Si $h\geq {\frac {D+d}{2}}$ , alors

$S=\int _{0}^{x_{2}}2c\ \mathrm {d} x$

Tonneau debout

La génératrice est la parabole

$0<h<L$

$S=\pi y^{2}=\pi \left({\frac {2(d-D)}{L^{2}}}\left({\frac {L}{2}}-h\right)^{2}+{\frac {D}{2}}\right)^{2}$

Si $h=0$ le tonneau est vide, et si $h=L$ le tonneau est plein.

Voir aussi

Bibliographie

Grand dictionnaire universel du XIX^e siècle par Pierre Larousse, à l'article Tonneau.
Quadrature, magazine de mathématiques pures et épicées, n^o 75, janvier-mars 2010, EDP Sciences. Le jaugeage des tonneaux : un jardin secret en mathématiques pures et appliquées, par François Jongmans.

Liens externes

Site perso de Michel Berteau - Volume du tonneau
Règles à calcul
Encyclopédie ou Dictionnaire universel raisonné des connoissances humaines, Fortuné Barthélemy de Félice, 1773, volume 24, à l'article Jaugeage.

Notes et références

Manuel pratique et élémentaire des poids et mesures, et du calcul décimal, p. 409 sur Google Livres, par Sébastien-André Tarbé des Sablons, Paris, 1809. La deuxième formule est donnée par le Grand dictionnaire universel du XIX^e siècle de Pierre Larousse.
Mémoire sur la théorie du jaugeage, p. 383 sur Google Livres par M. Dez, professeur royal de mathématiques à l'École royale militaire, in Mémoires de mathématique et de physique, Paris 1773

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.