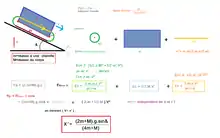
Tank à chenille
L'exercice du tank à chenille est un ancien exercice traditionnel du baccalauréat, en mécanique des systèmes simples.
Énoncé
Soit un plan incliné d'angle ; un tank est lâché sans vitesse initiale. Trouver son accélération par application du théorème de l'énergie cinétique.
Le tank est de masse totale m + M, la chenille étant de masse M ; l'entre-axes des roues est a, le rayon des roues est r.
Solution
L'énergie cinétique de translation est : 1/2 (m+M)V².
L'énergie de rotation de la chenille dans le référentiel du centre de masse est 1/2 M (V/2)².
On en déduit la solution :
a = g sin.(m+M) /(m+M.2)
Démonstration
En effet, chaque élément de la chenille tourne à la vitesse V dans le Rg.
L'Ec totale vaut donc : 1/2 (m +M.2) V².
Comme la chenille tourne sans glisser sur le plan incliné, le travail de la force du plan incliné sur le plan est nul.
La conservation de l'énergie donne donc : Ec +(m+M)gz = cste, d'où le résultat précédent par dérivation.
L'entre-axes des roues, a, ne joue aucun rôle, ni le rayon, r, des roues.
Réduisons par la pensée la masse du châssis, m, comme négligeable : on trouve 1/2 : pertinent avec le cas a = 0, car alors il s'agit d'une jante descendant un plan incliné (1/2Mr²(V/r)²+1/2MV²).