Tétracorde
Le tétracorde est un polycorde formé par quatre sons successifs d'une échelle musicale. C'est un outil qui permet de décrire les gammes et modes usuels de la musique occidentale. Il permet également de construire de nouvelles échelles musicales appelées gammes synthétiques.
Histoire
Le terme tétracorde est emprunté à la musique de la Grèce antique. Il désigne une succession de quatre notes. Deux tétracordes mis bout-à-bout forment une échelle musicale[1]. Ce concept est repris au Moyen Âge avec le système de l'octoéchos utilisé pour la construction des échelles mélodiques du chant grégorien. Dans le contexte de la musique tonale et du tempérament égal, on précise que le tétracorde doit être agencé en deux intervalles d'un ton et un intervalle d'un demi-ton[2]. Aujourd'hui, et notamment dans la théorie du jazz, la délimitation à un intervalle de quarte juste est abandonnée. Ceci permet d'utiliser la notion de tétracorde pour décrire de manière aisée tous les modes des systèmes courants tels que le système mineur mélodique, le système mineur harmonique et le système majeur harmonique.
Nomenclature
Ron Miller propose une nomenclature des différents tétracordes[3] :
| Nom | demi-tons | Nom | demi-tons |
|---|---|---|---|
| Lydien | 2 2 2 | Hongrois majeur | 1 3 2 |
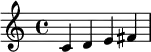 |
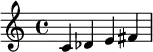 | ||
| Ionien | 2 2 1 | Hongrois mineur | 2 1 3 |
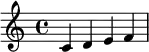 |
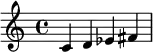 | ||
| Dorien | 2 1 2 | Harmonique | 1 3 1 |
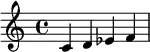 |
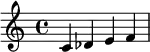 | ||
| Phrygien | 1 2 2 | Phrygien espagnol | 1 2 1 |
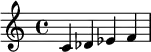 |
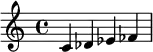 |
Les tétracordes hongrois majeur et mineur sont empruntés aux gammes de la musique traditionnelle hongroise. Ces gammes sont harmonisées et fonctionnent donc de manière similaire aux gammes issues du système tonal majeur-mineur. La tradition classique ne retient que les tétracordes contenus dans une quarte juste, à savoir, les tétracordes ioniens, doriens, phrygiens et harmoniques[4].
Cette nomenclature permet de résumer de manière commode la structure de n'importe quelle échelle heptatonique en demi-tons.
Analyse des échelles heptatoniques
Une échelle heptatonique est décomposable en deux tétracordes séparés par un intervalle intertétracordal.
| Tétracorde inférieur | intervalle intertétracordal | Tétracorde supérieur | |
|---|---|---|---|
| Intervalles | ton, ton, demi-ton | ton | ton, ton, demi-ton |
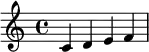 |
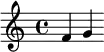 |
 |
Le tableau suivant montre la structure de tous les modes du système majeur, communément appelés modes ecclésiastiques, ainsi que leurs intervalles successifs exprimées demi-tons :
| Tétracorde inférieur | intervalle intertétracordal | Tétracorde supérieur | |
|---|---|---|---|
| Ionien | Majeur | ton | Majeur |
| 2 2 1 | 2 | 2 2 1 | |
| Dorien | Dorien | ton | Dorien |
| 2 1 2 | 2 | 2 1 2 | |
| Phrygien | Phrygien | ton | Phrygien |
| 1 2 2 | 2 | 1 2 2 | |
| Lydien | Lydien | demi-ton | Majeur |
| 2 2 2 | 1 | 2 2 1 | |
| Mixolydien | Majeur | ton | Dorien |
| 2 2 1 | 2 | 2 1 2 | |
| Aeolien | Dorien | ton | Phrygien |
| 2 1 2 | 2 | 1 2 2 | |
| Locrien | Phrygien | demi-ton | Lydien |
| 1 2 2 | 1 | 2 2 2 |
Construction de gammes synthétiques
Les gammes synthétiques sont inventées à partir des gammes usuelles. Le mélange de tétracordes est une des techniques permettant de construire de nouvelles gammes. En assemblant les noms des tétracordes utilisés on obtient le nom de la nouvelle gamme[4].
| Tétracorde inférieur | Tétracorde supérieur | ||
|---|---|---|---|
| Noms | Phrygien | ton | Majeur |
| Demi-tons | 1 2 2 | 2 | 2 2 1 |
| Exemple en do | 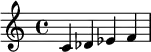 |
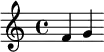 |
 |
| Tétracorde inférieur | Tétracorde supérieur | ||
|---|---|---|---|
| Noms | Majeur | ton | Harmonique |
| Demi-tons | 2 2 1 | 2 | 1 3 1 |
| Exemple en do | 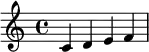 |
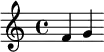 |
 |
| Tétracorde inférieur | Tétracorde supérieur | ||
|---|---|---|---|
| Noms | Harmonique | ton | Harmonique |
| Demi-tons | 1 3 1 | 2 | 1 3 1 |
| Exemple en do | 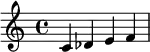 |
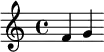 |
 |
Articles connexes
Notes et références
- Denis Arnold, Dictionnaire encyclopédique de la musique, vol. 2, Paris, Robert Lafont, , 987 p. (ISBN 9782221056554), p. 809
- A. Danhauser, Théorie de la Musique, Paris, Editions Henry Lemoine, , 195 p., p. 57
- (en) Ron Miller, Modal Jazz, composition & harmony, Advance Music, p. 16
- Siron, Jacques, 1949-, La partition intérieure : jazz, musiques improvisées, Outre Mesure, (ISBN 2907891030, OCLC 422845909, lire en ligne), p. 497