Surface minimale de Catalan
En géométrie différentielle, une surface minimale de Catalan est une surface minimale qui a été étudiée par Eugène Charles Catalan en 1855[1].
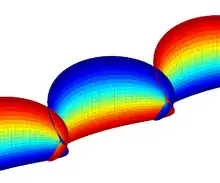
Surface minimale de Catalan.
La surface a pour équations paramétriques[2] :
Si l'on pose dans la paramétrisation ci-dessus, on obtient :
- Les lignes avec le paramètre fixé, se projettent sur le plan en des trochoïdes.
- Les lignes avec le paramètre fixé, sont des paraboles.
- La section de la surface par le plan (c'est-à-dire ) est une cycloïde.
Liens externes
- Robert Ferréol, « Surface minimale de Catalan », sur mathcurve
- (en) Eric W. Weisstein, « Catalan's Surface », sur MathWorld
- (en) Weiqing Gu, « Catalan's Minimal Surface », sur The Library of Surfaces
Bibliographie
(en) Ulrich Dierkes, Stefan Hildebrandt (de) et Friedrich Sauvigny (de), Minimal Surfaces, vol. 1, Berlin, Springer, coll. « Grundl. math. Wiss. » (no 339), , 692 p. (ISBN 978-3-642-11697-1, lire en ligne), p. 171 sq.
Références
- E. Catalan, « Mémoire sur les surfaces dont les rayons de courbures en chaque point, sont égaux et les signes contraires », C. r. hebd. séances Acad. sci., vol. 41, 1855, p. 1019-1023 et 1155 [lire en ligne].
- (en) Alfred Gray, Modern Differential Geometry of Curves and Surfaces with Mathematica, Boca Raton, CRC Press, 2e éd., 1997, p. 692-693 (« Catalan's Minimal Surface »).
Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.






