Suite de pliage de papier

Soit ${\displaystyle (w_{n})}$ la suite de mots sur ${\displaystyle \{0,1\}}$ définie par :

• ${\displaystyle w_{0}=\varepsilon }$ (le mot vide)
• ${\displaystyle w_{n+1}=w_{n}0w_{n}'}$, où ${\displaystyle x'}$ désigne le mot obtenu en prenant le retourné de ${\displaystyle x}$, et en échangeant les ${\displaystyle 0}$ et les ${\displaystyle 1}$.

Les premiers mots de la suite sont :

${\displaystyle {\begin{array}{l}w_{0}=\varepsilon \\w_{1}=0\\w_{2}=001\\w_{3}=0010011\\w_{4}=001001100011011\\w_{5}=0010011000110110001001110011011\end{array}}}$

La suite de pliage est la limite de cette suite de mots. C'est le mot infini :

${\displaystyle p=0010011000110110001001110011011\cdots }$

On peut montrer que la valeur ${\displaystyle p(n)}$ du ${\displaystyle n}$-ième symbole du mot ${\displaystyle p}$ se calcule récursivement par les formules :

${\displaystyle {\begin{array}{l}p(4n)=0\\p(4n+2)=1\\p(2n+1)=p(n)\end{array}}}$

Ainsi ${\displaystyle p(12)=0}$ et ${\displaystyle p(13)=p(6)=1}$. Ces formules se traduisent en un autre procédé de construction. On commence par une suite alternée de 0 et de 1, séparée par des « trous ». Dans un deuxième temps, ces trous sont remplis, à leur tour, par une suite alternée de 0 et de 1 lacunaire, etc. La suite résultante est la suite de pliage :

0 . 1 . 0 . 1 . 0 . 1 . 0 . 1 . 0 . 1 . 0 . 1 . 0 . 1 . 0 . 1 . 0 . 1 . 0 . 1 .  
  0   .   1   .   0   .   1   .   0   .   1   .   0   .   1   .   0   .   1   .
      0       .       1       .       0       .       1       .  
              0               .               1 

d'où la suite totale :

0 0 1 0 0 1 1 0 0 0 1 1 0 1 1.

Automate du pliage de papier régulier. Les états jaunes produisent un 0, les autres un 1.

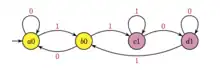
Comme la suite des pliages est automatique, elle est engendrée par un automate. On voit sur l'automate ci-contre que 01 conduit, depuis tout état, à l'état ${\displaystyle b0}$, donc que ${\displaystyle p(4n+1)=0}$; de même, 11 conduit à l'état ${\displaystyle c1}$, donc ${\displaystyle p(4n+3)=1}$.

La suite de pliage est un mot 2-morphique. Le morphisme 2-uniforme sur l'alphabet à quatre lettres ${\displaystyle \{a,b,c,d\}}$ engendré par le morphisme

${\displaystyle {\begin{array}{lcl}a\mapsto ab\\b\mapsto cb\\c\mapsto ad\\d\mapsto cd\end{array}}}$

à partir de la lettre ${\displaystyle a}$ est

${\displaystyle abcbadcbabcdadcb\cdots }$

ce qui donne le mot ${\displaystyle p}$ en envoyant ${\displaystyle a}$ et ${\displaystyle b}$ sur ${\displaystyle 0}$ et ${\displaystyle c}$ et ${\displaystyle d}$ sur ${\displaystyle 1}$.

On a

${\displaystyle {\begin{array}{lcl}p(4n)=0\\p(4n+2)=1\\p(2n+1)=p(n)\end{array}}}$

Le 2-noyau a donc trois éléments: la suite ${\displaystyle p}$, la suite constante égale à 1, et la suite constante égale à 0.

Soit

${\displaystyle G(X)=\sum _{n=1}^{\infty }p(n)X^{n}}$

la série formelle génératrice. La construction par récurrence implique que

${\displaystyle G(X)=\sum _{n=0}^{\infty }X^{4n+2}+\sum _{n=1}^{\infty }p(n)X^{2n+1}={\frac {X^{2}}{1-X^{4}}}+XG(X^{2})}$

Sur le corps des fractions rationnelles ${\displaystyle F_{2}((X))}$, on a

${\displaystyle G(X^{2})=G(X)^{2}}$

donc ${\displaystyle Y=G(X)}$ vérifie l'équation

${\displaystyle XY^{2}+Y+{\frac {X^{2}}{1+X^{4}}}=0}$.

On note ${\displaystyle c_{p}(n)}$ le nombre de facteurs (ou blocs distincts) de longueur ${\displaystyle n}$ de la suite de pliage ${\displaystyle p}$. On a les valeurs suivantes :

${\displaystyle n}$	0	1	2	3	4	5	6	${\displaystyle \geq 7}$
${\displaystyle c_{p}(n)}$	1	2	4	8	12	18	23	${\displaystyle 4n}$

On a donc ${\displaystyle c_{p}(n)=4n}$ pour ${\displaystyle n\geq 7}$.

Il n'y a qu'un nombre fini de palindromes distincts qui sont facteurs de la suite ${\displaystyle p}$. Plus précisément, il n'y a pas de palindrome de longueur 14 ou plus qui est facteur de la suite ${\displaystyle p}$.

On utilise la définition originelle pour étendre la suite de pliage aux cas où l'on ne plie pas toujours dans le même sens. Une suite d'instructions de pliage est une suite ${\displaystyle f=(f_{n})}$ de valeurs 0 ou 1. On définit alors une suite ${\displaystyle (w_{n})}$ de mots sur ${\displaystyle \{0,1\}}$, dépendant de ${\displaystyle f}$, par :

• ${\displaystyle w_{0}=\varepsilon }$ (le mot vide)
• ${\displaystyle w_{n+1}=w_{n}f_{n}w_{n}'}$, où ${\displaystyle f_{n}}$ est la ${\displaystyle n}$-ième instruction de pliage.

La suite de pliage avec instructions ${\displaystyle f}$ est la limite, notée ${\displaystyle p_{f}}$, de cette suite de mots. Si la suite d'instructions ne contient que des 0, on obtient la suite de pliage régulière. On peut montrer que

• toutes les suites de pliage ${\displaystyle p_{f}}$ ont même complexité de facteurs;
• toutes les suites de pliage ${\displaystyle p_{f}}$ ont même complexité de palindromes;
• une suite de pliage ${\displaystyle p_{f}}$ est une suite automatique si et seulement si la suite d'instructions ${\displaystyle f}$ est ultimement périodique.

C'est le nombre[1] dont le développement binaire est le complémentaire de la suite de pliage. Il est donc égal à

${\displaystyle 1-\sum _{n=1}^{\infty }{\frac {p(n)}{2^{n}}}=\sum _{k=0}^{\infty }{\frac {8^{2^{k}}}{2^{2^{k+2}}-1}}=0{,}850\,736\ldots }$ (suite A143347 de l'OEIS).

Il est transcendant, comme tous les nombres irrationnels dont le développement dans une base est automatique.