Quickhull
En géométrie algorithmique, quickhull est un algorithme pour le calcul de l'enveloppe convexe. C'est un algorithme du type diviser pour régner.
Principe
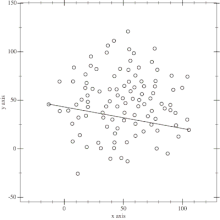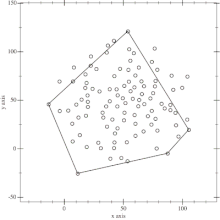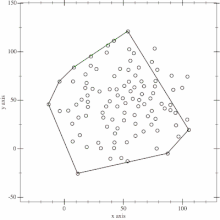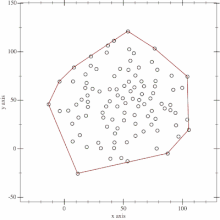
Remarquons d'abord que l'enveloppe convexe d'un ensemble E de points est définie par un sous-ensemble F de E. Le principe de l'algorithme est le suivant. En premier lieu, on trouve le point le plus à gauche P et le point le plus à droite Q (en cas d'égalité on choisit de manière arbitraire). Les points P et Q appartiennent à l'enveloppe convexe. On peut alors résoudre le problème en trouvant l'enveloppe convexe des points au-dessus de la droite (PQ) et celle des points en dessous de la droite, puis en concaténant les listes de points (en ne répétant pas P et Q). Les sous-problèmes ont alors une forme plus restreinte que l'instance d'origine : on dispose de deux points sur une droite, telle que tous les points sont du même côté de la droite, disons à gauche de (PQ), et tous les points qui appartiennent à la droite sont dans le segment [PQ]. On trouve alors le point H le plus éloigné de la droite. L'enveloppe convexe des points au-dessus de (PQ) s'obtient alors en concaténant l'enveloppe convexe des points à gauche de (PH) et celle des points à gauche de (HQ). On peut calculer récursivement ces ensembles (ils sont dans la même configuration que précédemment)[1].
- Les différentes étapes de l'algorithme Quickhull




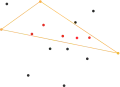

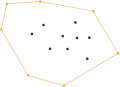
Complexité
L'algorithme a le même type de complexité en temps que l'algorithme de tri quicksort, c'est-à-dire dans le pire cas, et en moyenne[1].
Histoire
L'algorithme apparaît dans le livre Computational Geometry - An Introduction en 1985[2], où les auteurs attribuent les idées à plusieurs articles des années 1970[3] - [4] - [5].
Notes et références
- « Conception d’algorithmes et applications : Diviser pour Régner pour la Géométrie Algorithmique », sur Université Pierre-et-Marie-Curie,
- Franco P. Preparata et Michael Ian Shamos, Computational Geometry - An Introduction, Springer, (ISBN 3-540-96131-3, DOI 10.1007/978-1-4612-1098-6)
- William F. Eddy, « A New Convex Hull Algorithm for Planar Sets », ACM Trans. Math. Softw., vol. 3, no 4, , p. 398-403 (DOI 10.1145/355759.355766)
- Alex Bykat, « Convex Hull of a Finite Set of Points in Two Dimensions », Inf. Process. Lett., vol. 7, no 6, , p. 296-298 (DOI 10.1016/0020-0190(78)90021-2)
- P. J. Green et B. W. Silverman, « Constructing the Convex Hull of a Set of Points in the Plane », Comput. J., vol. 22, no 3, , p. 262-266 (DOI 10.1093/comjnl/22.3.262)
Liens externes
- Jakob Westhoff, « Calculate a convex hull - The QuickHull algorithm », une explication détaillée et un exemple d'application.
- Jeff Sember, « QuickHull algorithm (vidéo) » Vidéo d'une execution pas à pas de l'algorithme.

