Puzzle de Slothouber–Graatsma

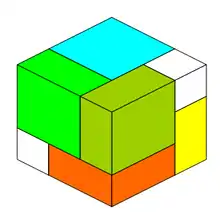
Solution partielle du puzzle de Slothouber-Graatsma montrant les six blocs de 1 x 2 x 2 en vue éclatée.

Solution complète du puzzle de Slothouber-Graatsma montrant tous les blocs vue éclatée.

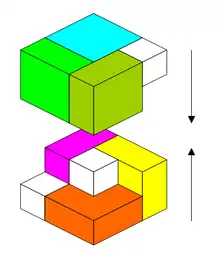
Le puzzle est essentiellement le même, si les trois blocs de 1 × 1 × 1 sont laissés de côté, de sorte que la tâche devient d'empiler les six blocs de 1 × 2 × 2 dans une boîte cubique.

La solution du puzzle de Slothouber–Graatsma devient simple lorsque l'on s'aperçoit que les trois blocs 1 × 1 × 1 (ou les trois trous) doivent être placés le long du corps de la diagonale de la boîte avec chacune des couches 3 x 3 dans les différentes directions doit contenir un tel bloc. Cela découle des considérations de parité, parce que les grands blocs ne peuvent remplir un nombre pair de neuf cellules dans chacune des couches 3 × 3[1].

Le puzzle de Slothouber–Graatsma est un exemple d'empilement de cube à l'aide polycubes convexes. Plus généralement des énigmes impliquant l'empilement de blocs convexes rectangulaires existent. L'exemple le plus connu est le puzzle de Conway qui demande l'empilement de dix-huit blocs convexes rectangulaires dans une boîte de 5 x 5 x 5. Un problème d'empilement plus complexe de blocs convexes rectangulaires est d'empiler quarante-et-un blocs de 1 x 2 x 4 dans une boîte de 7 x 7 x 7 (ce qui laisse 15 trous) ; la solution est analogue au cas  5 x 5 x 5, et ont trois trous cubiques de 1 x 1 x 5 dans des directions perpendiculaires couvrant les 7 couches.

• The Slothouber-Graatsma puzzle in Stewart Coffin's "The Puzzling World of Polyhedral Dissections"
• William Graatsma and Jan Slothouber: Dutch mathematical art