Projection de Cassini

La projection de Cassini (parfois aussi connue sous le nom Cassini-Soldner ou projection de Solder[1]) est une projection cartographique décrite par César-François Cassini de Thury en 1745[2]. Elle est transverse vis-à-vis de la projection équirectangulaire, dans le sens où il est possible de la voir comme l'application de la projection équirectangulaire après avoir tourné le globe de manière que la méridienne centrale devienne l'équateur.

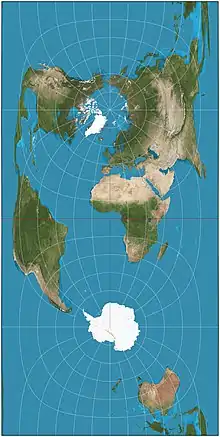
La projection du monde avec Cassini.

En considérant que la terre est une sphère, la projection est composée des opérations suivantes :

x=\arcsin(\cos \varphi \sin \lambda )\qquad y=\arctan \left({\frac {\tan \varphi }{\cos \lambda }}\right)

où λ est la longitude relative au méridien central et φ est la latitude. Lorsque ces équations sont programmées, la fonction arc tangente est en réalité la fonction atan2, avec pour premier argument sin (φ) et pour second argument cos φ cos λ.

Pour inverser cette projection, les opérations suivantes sont effectuées :

\phi =\arcsin(\sin(y+\phi _{0})\cos(x))\qquad \lambda =\arctan 2(\tan(x),\cos(y+\phi _{0}))

Dans la pratique, les modèles d'ellipsoïde ont toujours été appliqués avec cette projection, ce qui complique beaucoup son développement mathématique mais qui est utile à la pratique de l'arpentage. Néanmoins, l'usage de la projection de Cassini a été complètement supplantée par la projection de Mercator au moins dans les agences les plus importantes réalisant de la cartographie.

Distorsions

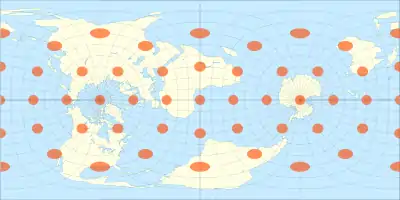
La projection de Cassini avec les indicatrices de déformation de Tissot.

Les zones placées le long du méridien central, et à leur perpendiculaire, se voient conserver les distances. Partout ailleurs, la distorsion est importante dans la direction nord-sud, et varie suivant le carré de la distance depuis le méridien central. Ainsi, plus la zone s'étire longitudinalement, plus la distorsion est constatée.

Ainsi, la projection de Cassini fonctionne mieux avec les zones étroites, et moins avec les zones larges.

Forme elliptique

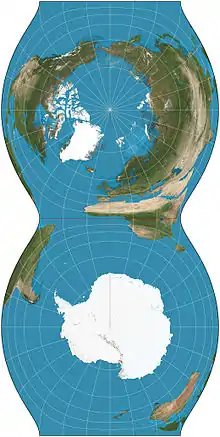
La projection du monde avec Cassini modélisé avec une ellipsoïde très écrasée d'aplanissement 1:2 (= excentricité ^√3⁄₂).

La projection de Cassini est généralement connue sous sa forme sphérique, mais peut aussi être généralisée à un modèle en ellipsoïde.

Les opérations conduisant à la transformation dans cette projection sont les suivantes :

N=(1-e^{2}\sin ^{2}(\phi ))^{-1/2}

T=\tan ^{2}(\phi )

A=\lambda \cos(\phi )

C={\frac {e^{2}}{1-e^{2}}}cos^{2}(\phi )

x=N(A-T{\frac {A^{3}}{6}}-(8-T+8C)T{\frac {A^{5}}{120}})

y=M(\phi )-M(\phi _{0})+N\tan(\phi )({\frac {A^{2}}{2}}+(5-T+6C){\frac {A^{4}}{24}})

où M() représente la distance méridionale.

La projection inverse peut être réalisée en suivant ces opérations :

\phi '=M^{-1}(M(\phi _{0})+y)

Si $\phi '={\frac {\pi }{2}}$ alors $\phi =\phi '$ et $\lambda =0$

sinon calculer T et N comme précédemment en utilisant $\phi '$ puis

R=(1-e^{2})(1-e^{2}sin^{2}\phi ')^{-3/2}

D=x/N

\phi =\phi '-\tan \phi '{\frac {N}{R}}({\frac {D^{2}}{2}}-(1+3T){\frac {D^{4}}{24}})

\lambda ={\frac {(D-T{\frac {D^{3}}{3}}+(1+3T)T{\frac {D^{5}}{15}})}{\cos \phi '}}

Notes et références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Cassini projection » (voir la liste des auteurs).

(en) « Cassini-Soldner - Help », Environmental Systems Research Institute, Inc. (consulté le 9 juin 2016)
(en) John P. Snyder, Flattening the Earth : Two Thousand Years of Map Projections, 1993, 365 p. (ISBN 0-226-76747-7, lire en ligne), p. 74–76.

Liens externes

Table of examples and properties of all common projections, from radicalcartography.net
Ordnance Survey GeoFacts on the Cassini Projection
Cassini dans proj4

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.