Problème de l'éclairage
Le problème de l'éclairage est un problème mathématique résolu posé dans le début des années 1950 par Ernst G. Straus[1].
Énoncé
La question est de savoir si une pièce aux murs tapissés de miroirs peut être illuminée entièrement par un unique point lumineux. Une question équivalente consiste à se demander si une boule de billard ponctuelle et non soumise aux frottements peut atteindre n'importe quel point de la table de billard, peu importe la géométrie de celle-ci.
Solutions
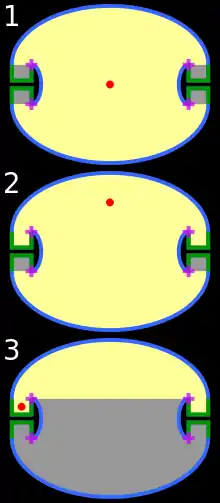
La première réponse est apportée en 1958 par Roger Penrose, qui décrète l'énoncé faux en fournissant en contre-exemple une pièce elliptique (image ci-contre). Il montre qu'une pièce de cette forme peut contenir des zones d'ombre, ce qui invalide l'énoncé de départ. Ce contre-exemple permet donc d'apporter une réponse à ce problème mathématique. Une seconde réponse est apportée en 1995 par Georges Tokarsky pour les pièces polygonales en deux dimensions, ce qui apporte des contraintes supplémentaires comme contre-exemple. La figure proposée est un polygone de 26 côtés qui possède comme propriété remarquable de n'avoir qu'un point d'ombre (ce qui est suffisant pour le considérer comme un contre-exemple)[2].
Finalement, David Castro améliore cette figure en 1997 pour ne la réduire qu'à un polygone de 24 côtés, mais avec les mêmes propriétés[3].

Vulgarisation
- Jérôme Cottanceau, Le choix du meilleur urinoir : Et 19 autres problèmes amusants qui prouvent que les maths servent à quelque chose !, Paris, Belin, coll. « Science à plumes », , 216 p. (ISBN 978-2-7011-9766-1), chap. 3 (« À quoi servent les maths... À (mal) éclairer sa chambre ? ») ;
- (en) [vidéo] Numberphile, The Illumination Problem sur YouTube.
Notes et références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Illumination problem » (voir la liste des auteurs).
- (en) Eric W. Weisstein, « Illumination Problem », sur Wolfram Research (consulté le ).
- (en) George Tokarsky, « Polygonal Rooms Not Illuminable from Every Point », American Mathematical Monthly, University of Alberta, Edmonton, Alberta, Canada, Mathematical Association of America, vol. 102, no 10, , p. 867–879 (DOI 10.2307/2975263, JSTOR 2975263).
- (en) David Castro, « Corrections », Quantum Magazine, Washington DC, Springer-Verlag, vol. 7, no 3, janvier–février 1997, p. 42.